
Cho tam giác ABC có M thuộc tia phân giác ngoài của góc C. Trên tia đối của tia CA lấy điểm I sao cho CI = CB.
a) So sánh MI với MB.
b) Chứng minh: MA + MB > AC + BC

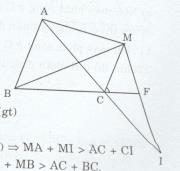
a) Gọi F là giao điểm của BC và MI
Ta có \(\widehat {MCB} = \widehat {MCA} + \widehat {ACB}\) và \(\widehat {MCI} = \widehat {MCF} + \widehat {FCI}\)
Advertisements (Quảng cáo)
Mà \(\widehat {MCA} = \widehat {MCF}\)(CM là tia phân giác của \(\widehat {ACF}\))
Và \(\widehat {ACB} = \widehat {FCI}\) (đối đỉnh). Do đó \(\widehat {MCB} = \widehat {MCI}\)
Xét ∆MCB và ∆MCI ta có MC (cạnh chung)
\(\widehat {MCB} = \widehat {MCI}\) và BC = CI (gt)
Do đó ∆MCB = ∆MCI (c.g.c) => MB = MI.
b) ∆AMI có MA + MI > AI (bất đằng thức trong tam giác) => MA + MI > AC + CI
Mà BC = CI, MB = MI (∆MCB = ∆MCI). Do đó MA + MB > AC + BC.
