
Cho tam giác \(ABC\) cân tại \(A\). Lấy điểm \(M,N\) lần lượt trên cạnh \(AB,AC\) sao cho \(AM = AN\).
a) Chứng minh tứ giác \(BMNC\) là hình thang cân
b) Xác định vị trí các điểm \(M,N\) để \(BM = MN = NC\).

Dựa vào định nghĩa của hình thang cân:
- Hình thang là tứ giác có hai cạnh đối song song
- Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

Advertisements (Quảng cáo)
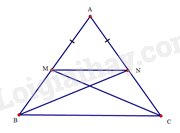
a) Vì hai tam giác \(AMN\) và \(ABC\) đều cân tại \(A\) nên
\(\widehat {AMN} = \widehat {ABC}\) (cùng bằng \(\frac{{180^\circ - \widehat A}}{2}\))
Mà \(\widehat {AMN}\) và \(\widehat {ABC}\) nằm ở vị trí đồng vị, suy ra \(MN//BC\).
Tứ giác \(BMNC\) có \(MN//BC\) và \(\widehat {MBC} = \widehat {NCB}\) nên \(BMNC\) là hình thang cân.
b) Do \(BM = MN\) nên tam giác \(MBN\) cân tại \(M\). Suy ra \(\widehat {MNB} = \widehat {MBN}\). Mà \(\widehat {MNB} = \widehat {NBC}\) (hai góc so le trong), suy ra \(\widehat {MBN} = \widehat {NBC}\). Do đó, \(BN\) là tia phân giác của góc \(ABC\).
Chứng minh tương tự ta được \(CM\) là tia phân giác của góc \(ACB\).
Dễ thấy, nếu các điểm \(M,N\) được xác định sao cho \(BM,CN\) lần lượt là tia phân giác của góc \(ABC,ACB\) thì \(BN = MN = CN\).
Vậy \(M\) là giao điểm của \(AB\) và tia phân giác của góc \(ACB,N\) là giao điểm của \(AC\) và tia phân giác của góc \(ABC\) thì \(BN = MN = CN\).
