
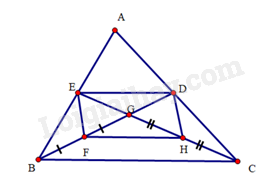
Cho tam giác \(ABC\) có các đường trung tuyến \(BD,CE\) cắt nhau tại \(G\). Gọi \(F,H\) lần lượt là trung điểm của \(BG,CG\).
a) Tứ giác \(EFHD\) là hình gì? Vì sao?
b) Tìm điều kiện của tam giác \(ABC\) để tứ giác \(EFHD\) là hình vuông.

Dựa vào dấu hiệu nhận biết của hình bình hành và hình vuông để xác định tứ giác \(EFHD\)

Advertisements (Quảng cáo)
a) Do \(G\) là trọng tâm tam giác \(ABC\) nên \(DG = \frac{1}{2}BG,EG = \frac{1}{2}CG\). Mà \(F,H\) lần lượt là trung điểm của \(BG,CG\) nên \(DG = BF = FG,EG = CH = HG\).
Tứ giác \(EFHG\) có hai đường chéo \(EH\) và \(DF\) cắt nhau tại trung điểm của mỗi đường nên \(EFHG\) là hình bình hành.
b) Để hình bình hành \(EFHG\) là hình vuông thì \(EH = DF\) và \(EH \bot DF\)
suy ra \(BG = CG,EG = DG\) và \(BD \bot CE\).
\(\Delta BEG = \Delta CDG\) (c.g.c). Suy ra \(BE = CD\). Mà \(AB = 2BE,AC = 2CD\), suy ra \(AB = AC\).
Dễ thấy nếu \(AB = AC\) và \(BD \bot CE\) thì tứ giác \(EFHG\) là hình vuông.
Vậy tam giác \(ABC\) cân tại \(A\) có đường trung tuyến \(BD\), \(CE\) vuông góc với nhau thì tứ giác \(EFHG\) là hình vuoogn.
