Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó.. Câu 51 trang 166 Sách bài tập (SBT) Toán 8 tập 1 - Ôn tập chương II - Đa giác - Diện tích đa giác
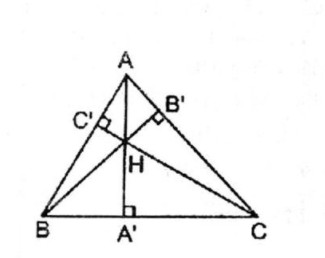
Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó.
Chứng minh rằng \({{HA’} \over {AA’}} + {{HB’} \over {BB’}} + {{HC’} \over {CC’}} = 1\)
Advertisements (Quảng cáo)
\(\eqalign{ & {S_{HBC}} + {S_{HAC}} + {S_{HAB}} = {S_{ABC}} \cr & \Rightarrow {{{S_{HBC}}} \over {{S_{ABC}}}} + {{{S_{HABC}}} \over {{S_{ABC}}}} + {{{S_{HAB}}} \over {{S_{ABC}}}} = 1 \cr} \)
Suy ra: \({{HA’.BC} \over {AA’.BC}} + {{HB’.AC} \over {BB’.AC}} + {{HC’.AB} \over {CC’.AB}} = 1\)
\( \Rightarrow {{HA’} \over {AA’}} + {{HB’} \over {BB’}} + {{HC’} \over {CC’}} = 1\)