a. Các tam giác DAC và DCK
b. Tam giác DAC và tứ giác ADLB
c. Các tứ giác ABKD và ABLD
. Câu 55 trang 166 Sách bài tập (SBT) Toán 8 tập 1 - Ôn tập chương II - Đa giác - Diện tích đa giác
Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc cạnh BC sao cho BK = KL = LC. Tính tỉ số diện tích của :
a. Các tam giác DAC và DCK
b. Tam giác DAC và tứ giác ADLB
c. Các tứ giác ABKD và ABLD
Giải:
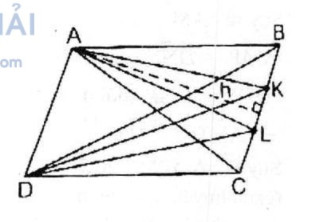
Ta có: \({S_{ACD}} = {S_{BCD}} = {S_{DAB}} = {S_{CAB}} = {1 \over 2}{S_{ABCD}}\) (1)
\(CK = {1 \over 2}CB\)
∆ DCK = ∆ DCB có chung chiều cao kẻ từ đỉnh D, cạnh đáy \(CK = {2 \over 3}CB\)
Advertisements (Quảng cáo)
\( \Rightarrow {S_{DCK}} = {2 \over 3}{S_{DBC}}\) (2)
Từ (1) và (2) suy ra: \({S_{DCK}} = {2 \over 3}{S_{DAC}} \Rightarrow {{{S_{DCK}}} \over {{S_{DAC}}}} = {2 \over 3}\)
b. Ta có: \({S_{ADLB}} = {S_{ADB}} + {S_{DLB}}\)
∆ DBC và ∆ DLC có chung chiều cao kẻ từ đỉnh D, cạnh đáy \(LB = {2 \over 3}BC\)
\( \Rightarrow {S_{DLB}} = {2 \over 3}{S_{DBC}}\)
mà \({S_{DAC}} = {S_{ADB}} = {S_{DBC}}\) (chứng minh trên)
Suy ra: \({S_{ADLB}} = {S_{DAC}} + {2 \over 3}{S_{DAC}} = {5 \over 3}{S_{DAC}} \Rightarrow {{{S_{DAC}}} \over {{S_{ADLB}}}} = {3 \over 5}\)
c. Ta có: \({S_{ABKD}} = {S_{ABD}} + {S_{DKB}}\)
∆ DKB và ∆ DCB có chung chiều cao kẻ từ D, cạnh đáy \(BL = {1 \over 3}BC\)
\( \Rightarrow {S_{DKB}} = {1 \over 3}{S_{DCB}}\)
mà \({S_{DAC}} = {S_{ADB}} = {S_{DBC}}\) (chứng minh trên)
\( \Rightarrow {S_{ABKD}} = {S_{DAC}} + {1 \over 3}{S_{DAC}} = {4 \over 3}{S_{DAC}} \Rightarrow {{{S_{ABKD}}} \over {{S_{ADLB}}}} = {{{4 \over 3}{S_{DAC}}} \over {{5 \over 3}{S_{DAC}}}} = {4 \over 5}\)
