Qua tâm O của hình vuông ABCD cạnh a, kẻ đường thẳng \(l\) cắt cạnh AB và CD lần lượt tại M và N. Biết MN = b. Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng \(l\) theo a và b (a và b có cùng đơn vị đo)

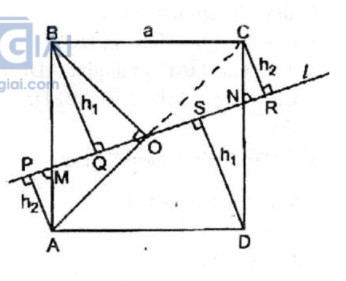
Gọi h1 và h2 là khoảng cách từ đỉnh B và đỉnh A đến đường thẳng\(l\);
Tổng khoảng cách là S. Vì O là tâm đối xứng của hình vuông.
⇒ OM = ON (tính chất đối xứng tâm)
Suy ra: AM = CN
\(\widehat {AMP} = \widehat {DNS}\) (đồng vị)
\(\widehat {DNS} = \widehat {CNR}\) (đối đỉnh)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {AMP} = \widehat {CNR}\)
Suy ra: ∆ APM = ∆ CRN (cạnh huyền, góc nhọn)
⇒ CR = AP = h2
AM = CD ⇒ BM = DN
\(\widehat {BMQ} = \widehat {DNS}\) (so le trong)
Suy ra: ∆ BQM = ∆ DSN (cạnh huyền, góc nhọn) ⇒ DS = BQ = h1
\(\eqalign{ & {S_{BOA}} = {1 \over 4}{S_{AOB}} = {1 \over 4}{a^2}(1) \cr & {S_{BOA}} = {S_{BOM}} + {S_{AOM}} = {1 \over 2}{b \over 2}.{h_1} + {1 \over 2}{b \over 2}.{h_2} = {b \over 4}\left( {{h_1} + {h_2}} \right)(2) \cr} \)
Từ (1) và (2): ${h_1} + {h_2} = {{{a^2}} \over b}\)
\(S = 2\left( {{h_1} + {h_2}} \right) = {{2{a^2}} \over b}\)
