
a) Ở hình a, cho biết \(\widehat N = \widehat E,\,\,\widehat M = \widehat D,\,\,MP = 18,\,\,\)\(DF = 24.\) Tính y
b) cho hình thang ABCD (hình b). Hãy điền vào chỗ trống:
\(\Delta AMB \sim \Delta .....;\)
\({{AM} \over {.....}} = {{.....} \over {DC}} = {{MB} \over {.....}};\,\,x = ...;\,\,\,y = ...\,\,\,\)
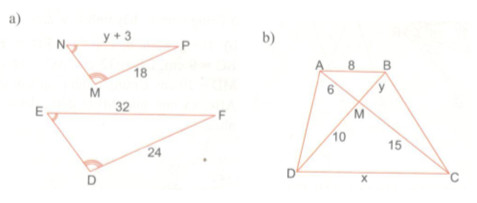

a) Xét ∆MNP và ∆EDF có: \(\widehat N = \widehat E(gt)\) và \(\widehat M = \widehat D(gt)\)
\(\Rightarrow \Delta MNP \sim \Delta DEF(g.g)\)
\( \Rightarrow {{MP} \over {DF}} = {{NP} \over {EF}} \)
Advertisements (Quảng cáo)
\(\Rightarrow {{18} \over {24}} = {{y + 3} \over {32}} \)
\(\Rightarrow {3 \over 4} = {{y + 3} \over {32}} \)
\(\Rightarrow 4(y + 3) = 96 \)
\(\Rightarrow y + 3 = 24 \Rightarrow y = 21.\)
b) • \(\Delta AMB \sim \Delta CMD\) vì \(\widehat {AMB} = \widehat {CMD}\) (hai góc đối đỉnh) và \(\widehat {MAB} = \widehat {MCD}\) (hai góc so le trong và AB // CD)
• \({{AM} \over {CM}} = {{AB} \over {DC}} = {{MB} \over {MD}} \Rightarrow {6 \over {15}} = {8 \over x} = {y \over {10}}\)
Từ đó suy ra:
\(\eqalign{ & {6 \over {15}} = {8 \over x} \Rightarrow x = 20 \cr & {6 \over {15}} = {y \over {10}} \Rightarrow y = 4 \cr} \)
