
Tính diện tích hình thang cân có hai đáy bằng 23 cm, 13 cm và cạnh bên bảng 13 cm.

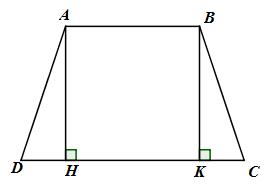
Vẽ \(AH \bot CD\) tại H và \(BK \bot CD\) tại K
\( \Rightarrow AK//BK\)
Mà \(AB//CD\,\,\left( {gt} \right)\)
Do đó tứ giác ABKH là hình bình hành.
\( \Rightarrow HK = AB = 13\,\,\left( {cm} \right)\)
Advertisements (Quảng cáo)
Xét tam giác \(HAD\,\,\left( {\widehat {AHD} = {{90}^0}} \right)\) và tam giác \(KBC\,\,\left( {\widehat {BKC} = {{90}^0}} \right)\) có:
\(AD = BC,\,\,\widehat D = \widehat C\) (tứ giác ABCD là hình thang cân)
Do đó \(\Delta HAD = \Delta KBC\) (cạnh huyền – góc nhọn)
\( \Rightarrow DH = CK\).
Do đó \(DH = CK = {{CD - HK} \over 2} = {{23 - 13} \over 2} = 5\,\,\left( {cm} \right)\)
\(\Delta HAD\) vuông tại H \( \Rightarrow A{H^2} + D{H^2} = A{D^2}\) (Định lí Pytago)
Nên \(AH = \sqrt {A{D^2} - D{H^2}} = \sqrt {{{13}^2} - {5^2}} = 12\,\,\left( {cm} \right)\)
Vậy \({S_{ABCD}} = {1 \over 2}\left( {AB + CD} \right).AH = {1 \over 2}\left( {13 + 23} \right).12 = 216\,\,\left( {c{m^2}} \right)\)
