Bài tập - Chủ đề 4 : Diện tích đa giác - Bài tập 22 trang 170 Tài liệu dạy – học Toán 8 tập 1. Giải bài tập Chứng minh hai đường chéo của một hình bình hành luôn chia nó thành bốn tam giác có diện tích bằng nhau.

Chứng minh hai đường chéo của một hình bình hành luôn chia nó thành bốn tam giác có diện tích bằng nhau.

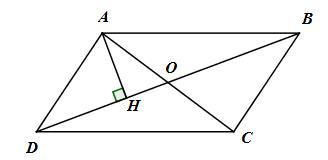
Gọi O là giao điểm của AC và BD, kẻ \(AH \bot DB\) tại H.
ABCD là hình bình hành \( \Rightarrow O\) là trung điểm của AC và BD.
Advertisements (Quảng cáo)
Ta có \({S_{ADO}} = {1 \over 2}AH.DO,\,\,{S_{ABO}} = {1 \over 2}AH.BO\)
Và \(DO = OB\) (O là trung điểm của BD)
Do đó \({S_{ADO}} = {S_{ABO}}\)
Lập luận tương tự ta có : \({S_{ADO}} = {S_{CDO}},\,\,{S_{CDO}} = {S_{BCO}}\)
Vậy \({S_{ADO}} = {S_{ABO}} = {S_{BCO}} = {S_{CDO}}\)
