Bài tập - Chủ đề 4 : Diện tích đa giác - Bài tập 16 trang 170 Tài liệu dạy – học Toán 8 tập 1. Giải bài tập Tính diện tích của hình thang ABCD (AB // CD) Cho bỉết AB 6 cm, BC = 10 cm, CD = 20 cm
Tính diện tích của hình thang ABCD \((AB // CD)\) Cho bỉết AB 6 cm, BC = 10 cm, CD = 20 cm và \(\widehat C = 30^\circ \) .
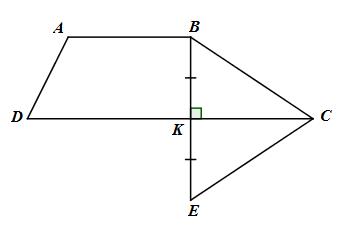
Gọi E là điểm đối xứng của B quan điểm K.
\(\Delta CBE\) có CK là đường cao, đường trung tuyến \( \Rightarrow \Delta CBE\) cân tại C.
\( \Rightarrow CK\) là tia phân giác của góc BCE.
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {BCE} = 2\widehat {BCD} = {2.30^0} = {60^0}\)
Do đó tam giác BCE đều \( \Rightarrow BE = BC = 10\,\,cm\)
Ta có \(BK = {1 \over 2}BE = {1 \over 2}.10 = 5\,\,\left( {cm} \right)\)
Tứ giác ABCD là hình thang (gt)
Do đó \({S_{ABCD}} = {1 \over 2}\left( {AB + CD} \right).BK = {1 \over 2}\left( {6 + 20} \right).5 = 65\,\,\left( {c{m^2}} \right)\)