Bài tập - Chủ đề 4 : Diện tích đa giác - Bài tập 14 trang 169 Tài liệu dạy – học Toán 8 tập 1. Giải bài tập Tính diện tích hình thang vuông ABCD có hai đáy AB = 6cm, CD = 9 cm và cạnh xiên BC = 5 cm.
Tính diện tích hình thang vuông ABCD có hai đáy AB = 6cm, CD = 9 cm và cạnh xiên BC = 5 cm.
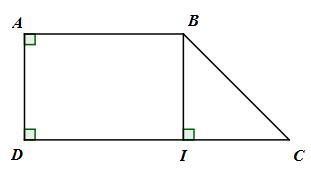
Kẻ \(BI \bot CD\) tại I.
Tứ giác ABID có :
\(\widehat {BAD} = {90^0},\,\,\widehat {ADI} = {90^0}\,\,\)(ABCD là hình thang vuông)
Advertisements (Quảng cáo)
Và \(\widehat {BID} = {90^0}\,\,(BI \bot CD\) tại I)
Do đó tứ giác ABID là hình chữ nhật \( \Rightarrow DI = AB = 6cm\)
\(IC = CD - DI = 9 - 6 = 3\,\,\left( {cm} \right)\)
\(\Delta BIC\) vuông tại I có \(B{I^2} + I{C^2} = B{C^2}\) (Định lí Pytago)
\( \Rightarrow B{I^2} + 9 = 25 \Leftrightarrow B{I^2} = 16 = {4^2} \Rightarrow BI = 4\,\,\left( {cm} \right)\)
\(S = {{\left( {AB + CD} \right).AD} \over 2} = {{\left( {6 + 9} \right).4} \over 2} = 30\,\,\left( {c{m^2}} \right)\)