
Cho tam giác ABC vuông tại A, M là tring điểm trên cạnh Ac. Kẻ \(MD \bot BC\)
a) Chứng minh rằng tam giác DMC đồng dạng với tam giác ABC.
b) Gọi E là giao điểm của đường thẳng AB với đường thẳng MD. Chứng minh rằng tam giác DBE đồng dạng với tam giác DMC.
c) Đường thẳng BM cắt EC ở K. Chứng minh rằng \(\Delta MEK \sim MBD\)

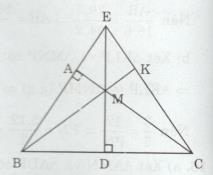
a) Xét ∆DMC và ∆ABC có: \(\widehat C\) (chung) và \(\widehat {MDC} = \widehat {BAC}( = 90^\circ ) \)
\(\Rightarrow \Delta DMC \sim \Delta ABC(g.g)\)
b) Xét ∆DBE và ∆DMC có \(\widehat {BDE} = \widehat {MDC}( = 90^\circ )\) và \(\widehat {DEB} = \widehat {DCM}\) (cùng phụ với góc B)
Advertisements (Quảng cáo)
\( \Rightarrow \Delta DBE \sim \Delta DMC(g.g)\)
c) Xét ∆BEC có ED và CA cắt nhau tại M (gt), ED là đường cao \((MD \bot BC,E \in DM)\)
Và CA là đường cao \((CA \bot BE\) tại A)
Suy ra M là trực tâm của tam giác BEC
Nên BK là đường cao của ∆BEC
\( \Rightarrow BK \bot EC\) tại K
Xét ∆MEK và ∆MBD có:
\(\widehat {EMK} = \widehat {BMD}\) (hai góc đối đỉnh) và \(\widehat {EKM} = \widehat {MDB}( = 90^\circ ) \)
\(\Rightarrow \Delta MEK \sim \Delta MBD(g.g)\)
