Bài tập - Chủ đề 2 : Tam giác đồng dạng và ứng dụng - Bài tập 18 trang 91 Tài liệu dạy – học Toán 8 tập 2. Giải bài tập Cho tam giác ABC nhọn có các đường cao BE, CF cắt nhau tại H.
Cho tam giác ABC nhọn có các đường cao BE, CF cắt nhau tại H.
a) Chứng minh rằng tam giác AEB đồng dạng với tam giác AFC. Suy ra \(AE.AC = AF.AB.\)
b) Chứng minh rằng \({{HE} \over {HC}} = {{HF} \over {HB}}\)
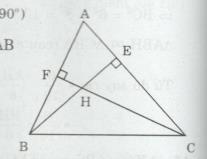
a) Xét ∆AEB và ∆AFC có: \(\widehat A\) chung và \(\widehat {AEB} = \widehat {AFC}( = 90^\circ )\)
Advertisements (Quảng cáo)
\( \Rightarrow \Delta AEB \sim \Delta AFC(g.g)\)
\(\Rightarrow {{AE} \over {AF}} = {{AB} \over {AC}} \Rightarrow AE.AC = AF.AB\)
b) Xét ∆HEC và ∆HBF có:
\(\widehat {EHC} = \widehat {BHF}\) (đối đỉnh) và \(\widehat {HEC} = \widehat {BFH}( = 90^\circ )\)
\( \Rightarrow \Delta HEC \sim \Delta HFB(g.g)\)
\(\Rightarrow {{HE} \over {HF}} = {{HC} \over {HB}} \Rightarrow {{HE} \over {HC}} = {{HF} \over {HB}}\)