Bài tập - Chủ đề 4 : Diện tích đa giác - Bài tập 20 trang 170 Tài liệu dạy – học Toán 8 tập 1. Giải bài tập Cho hình chữ nhật ABCD có diện tích 72 cm2. Gọi E và F lần lượt là trung điểm của AB và CD. Tính diện tích của các hình bình hành AECF, EBFD.
Cho hình chữ nhật ABCD có diện tích 72 cm2. Gọi E và F lần lượt là trung điểm của AB và CD. Tính diện tích của các hình bình hành AECF, EBFD.
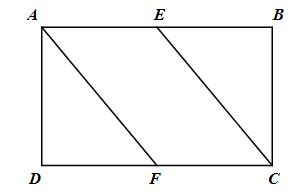
Ta có \(AE = EB = {{AB} \over 2}\) (E là trung điểm của AB)
\(CF = FD = {{CD} \over 2}\) (F là trung điểm của CD)
Và \(AB = CD\) (ABCD là hình chữ nhật)
Advertisements (Quảng cáo)
\( \Rightarrow AE = EB = CF = FD\)
Tứ giác AECF có : AE = CF
Và AE // CF \(\left( {AB//CD,\,\,E \in AB,\,\,F \in CD} \right)\)
\( \Rightarrow \) Tứ giác AECF là hình bình hành
\( \Rightarrow {S_{AECF}} = AD.CF \Rightarrow {S_{AECF}} = AD.{{CD} \over 2} = {{{S_{ABCD}}} \over 2} = {{72} \over 2} = 36\,\,\left( {c{m^2}} \right)\)