
Cho hình bình hành ABCD có AB 12 cm, AD = 24 cm và \(\widehat A = 30^\circ \). Tính diện tích của hình bình hành ABCD.

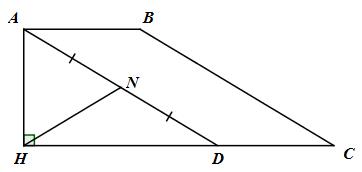
Gọi N là trung điểm của AD \( \Rightarrow AN = {{AD} \over 2} = {{24} \over 2} = 12\,\,\left( {cm} \right)\)
Kẻ \(AH \bot CD\) tại H.
Mà AB // CD (Tứ giác ABCD là hình bình hành)
Nên \(AH \bot AB\)
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {BAH} = {90^0} \Rightarrow \widehat {HAN} + \widehat {NAB} = {90^0}\)
\( \Rightarrow \widehat {HAN} + {30^0} = {90^0} \Rightarrow \widehat {HAN} = {90^0} - {30^0} = {60^0}\)
\(\Delta AHD\) vuông tại H có HN là đường trung tuyến (N là trung điểm của AD)
\( \Rightarrow HN = AN = {{AD} \over 2} \Rightarrow \Delta AHN\) cân tại N
Mà \(\widehat {HAN} = {60^0} \Rightarrow \Delta AHN\) đều \( \Rightarrow AH = AN = 12\,\,\left( {cm} \right)\)
\({S_{ABCD}} = AH.CD = 12.12 = 144\,\,\left( {c{m^2}} \right)\)
