
Cho tam giác ABC vuông tại A (AB < AC) có AH là đường cao. Vẽ \(HE \bot AB,HF \bot AC(E \in AB,F \in AC)\)
a) Chứng minh rằng AM = EF.
b) Gọi M là điểm đối xứng của H qua E. Chứng minh rằng tứ giác MAFE lả hình binh hành.
c) Gọi D là trung điẻm cùa HC, I là giao điểm của AH và EF. Chứng minh rằng BI vuông góc với AD.
d) Gọi N lả điểm đổi xứng của H qua F. Chứng minh rằng ba điểm M, A, N thẳng hàng.

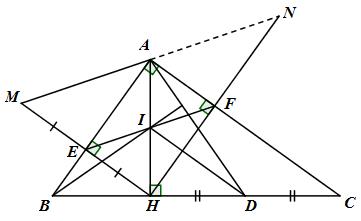
a) Tứ giác AEHF có:
\(\widehat {EAF} = {90^0}\,\,(\Delta ABC\) vuông tại A);
\(\widehat {AEH} = {90^0}\,\,(EH \bot AB\) tại E)
\(\widehat {AFH} = {90^0}\,\,(HF \bot AC\) tại F)
Do đó tứ giác AEHF là hình chữ nhật \( \Rightarrow AH \bot EF\).
b) Ta có \(AF = EH\) (AEHF là hình chữ nhật)
Và \(ME = EH\) (E là trung điểm của MH) \( \Rightarrow AF = ME\).
Mà AF // ME (AF // EH, \(M \in EH\)) nên AMEF là hình bình hành.
c) Hình chữ nhật AEHF có I là giao điểm của AH và EF (gt)
Advertisements (Quảng cáo)
\( \Rightarrow \) I là trung điểm của AH.
Mà D là trung điểm của HC
\( \Rightarrow ID\) là đường trung bình của tam giác AHC \( \Rightarrow ID//AC\).
Mặt khác \(AC \bot AB\,\,(\Delta ABC\) vuông tại A).
Do đó \(ID \bot AB\).
Xét tam giác ABD có DI là đường cao \(\left( {DI \bot AB} \right)\), AH là đường cao \(\left( {AH \bot BD} \right)\)
Và DI và AH cắt nhau tại I (gt).
Do đó I là trực tâm của tam giác ABD
\( \Rightarrow BI\) là đường cao của tam giác ABD \( \Rightarrow BI \bot AD\).
d) Xét tam giác MHN có:
E là trung điểm của MH (M đối xứng với H qua E)
F là trung điểm của HN (N đối xứng với H qua F)
\( \Rightarrow EF\) là đường trung bình của tam giác MHN \( \Rightarrow EF//MN\).
Mà \(EF//MA\) (MAFE là hình bình hành)
Do đó MN, MA trùng nhau (tiên đề Ơ-clit).
Vậy M, A, N thẳng hàng.
