
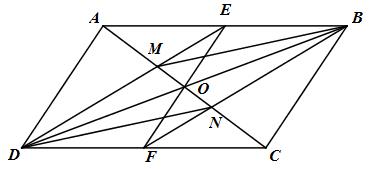
Cho hình bình hành ABCD, tâm O. Trên đường chéo AC lấy hai điểm M, N sao cho AM = MN = CN.
a) Chứng minh rằng hai điểm M và N đối xứng nhau qua tâm O.
b) Chứng minh rằng O là tâm đối xứng của tứ giác DMBN.
c) DM cắt AB tại E, BN cắt CD tại F. Chứng minh rằng hai điểm E và F đối xứng nhau qua O.

a) O là tâm của hình bình hành ABCD (gt)
\( \Rightarrow O\) là trung điểm của AC và BD \( \Rightarrow OA = OC\).
Mà \(AM = CN\,\,\left( {gt} \right)\) nên \(OA - AM = OC - CN\)
\( \Rightarrow OM = ON \Rightarrow O\) là trung điểm của MN
\( \Rightarrow M,N\) đối xứng nhau qua tâm O.
b) Tứ giác DMBN có DB và MN cắt nhau tại O (gt),
Advertisements (Quảng cáo)
O là trung điểm của DB (câu a)
Và O là trung điểm của MN (câu a)
Do đó tứ giác DMBN là hình bình hành
\( \Rightarrow O\) là tâm đối xứng của tứ giác DMBN.
c) Tứ giác DEBF có :
EB // CD (AB // CD, \(E \in AB,\,\,F \in CD\))
Và DE // EB (DM // BN, \(E \in BM,\,\,F \in BN\))
\( \Rightarrow \) Tứ giác DEBF là hình bình hành
\( \Rightarrow DB\) và EF cắt nhau tại trung điểm của mỗi đường.
Mà O là trung điểm của BD (câu a)
Nên O là trung điểm của EF \( \Rightarrow E,F\) đối xứng nhau qua O.
