Bài tập - Chủ đề 1 : Định lí Thales - Bài tập 7 trang 69 Tài liệu dạy – học Toán 8 tập 2. Giải bài tập Cho hình thang ABCD (AB // CD). Đường thẳng song song với AB cắt AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q. Chứng minh rằng MN = PQ.
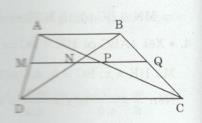
Cho hình thang ABCD (AB // CD). Đường thẳng song song với AB cắt AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q. Chứng minh rằng MN = PQ.
Xét ∆ABD có MN // AB (gt) \( \Rightarrow {{MN} \over {AB}} = {{DN} \over {DB}}\) (hệ quả của định lí Thales) (1)
Xét ∆BDC có NQ // DC (cùng song song với AB)
Advertisements (Quảng cáo)
\( \Rightarrow {{DN} \over {DB}} = {{CQ} \over {CB}}\) (hệ quả của định lý Thales) (2)
Xết ∆ABC có PQ // AB (gt)
\( \Rightarrow {{CQ} \over {CB}} = {{PQ} \over {AB}}\) (hệ quả của định lí Thales) (3)
Từ (1), (2) và (3) suy ra \({{MN} \over {AB}} = {{PQ} \over {AB}} \Rightarrow MN = PQ\)