
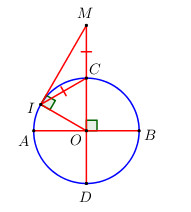
Cho hai đường kính vuông góc AB và CD của đường tròn (O; R). Gọi I là một điểm trên cung nhỏ AC sao cho tiếp tuyến qua I cắt DC kéo dài tại M và IC = CM.
a) Tính \(\widehat {AOI}\) .
b) Tính độ dài đoạn OM theo R.
a) Chứng minh tam giác OCI có \(\widehat {CIO} = \widehat {COI}\), từ đó suy ra tam giác OCI đều.
Sử dụng tính chất cộng góc \(\widehat {AOI} + \widehat {COI} = {90^0}\).
b) Chứng minh \(CM = CO\).
Advertisements (Quảng cáo)

a) Xét tam giác CMI có \(CI = CM\,\,\left( {gt} \right) \Rightarrow \Delta CIM\) cân tại C \( \Rightarrow \widehat {CIM} = \widehat {CMI}\) (hai góc ở đáy).
Mà \(\widehat {CIM} + \widehat {CIO} = \widehat {MIO} = {90^0}\).
\(\widehat {CMI} + \widehat {COI} = {90^0}\) (hai góc nhọn trong tam giác vuông phụ nhau)
\( \Rightarrow \widehat {CIO} = \widehat {COI} \Rightarrow \Delta CIO\) cân tại C \( \Rightarrow CO = CI\). Mà \(CO = OI = R \Rightarrow CO = OI = CI = R \Rightarrow \Delta CIO\) đều \( \Rightarrow \widehat {COI} = {60^0}\).
Mà \(\widehat {AOI} + \widehat {COI} = \widehat {AOM} = {90^0}\)
\( \Rightarrow \widehat {AOI} = {90^0} - \widehat {COI} = {90^0} - {60^0} = {30^0}\).
b) Ta có \(CM = CI = CO = R\,\,\left( {cmt} \right) \Rightarrow OM = OC + CM = 2R\).
