
Cho ba điểm A, B, C trên đường tròn (O). Tiếp tuyến tại A cắt dây cung CB kéo dài tại điểm M. Chứng minh: \(\widehat {AMC} = \widehat {ABC} - \widehat {ACB}\) .
+) Góc ngoài bằng tổng hai góc trong không kề với nó.
+) Góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung thì bằng nhau.
Advertisements (Quảng cáo)

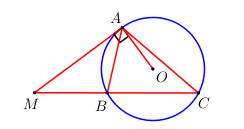
Xét tam giác ABM ta có \(\widehat {ABC} = \widehat {MAC} + \widehat {MAB}\) (góc ngoài bằng tổng hai góc trong không kề với nó).
Mà \(\widehat {MAB} = \widehat {ACB}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AB)
\( \Rightarrow \widehat {ABC} = \widehat {MAC} + \widehat {ACB} \Rightarrow \widehat {MAC} = \widehat {ABC} - \widehat {ACB}\) (đpcm).
