Chứng minh rằng hai trung tuyến kẻ từ \(B\) và \(C\) của tam giác \(ABC\) vuông góc với nhau khi và chỉ khi có hệ thức sau:
\(\cot A = 2(\cot B + \cot C).\)
Giải
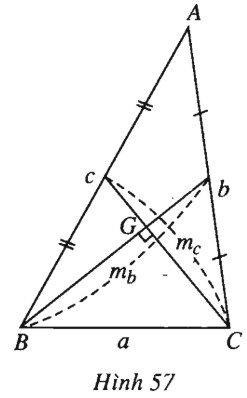
Gọi \(G\) là trọng tâm tam giác ABC (h.57).
Khi đó \(GB \bot GC \Leftrightarrow {a^2} = \dfrac{4}{9}\left( {m_b^2 + m_c^2} \right)\)
\(\begin{array}{l}\Leftrightarrow 9{a^2} = 4\left( {\dfrac{{{a^2} + {c^2}}}{2} - \dfrac{{{b^2}}}{4} + \dfrac{{{a^2} + {b^2}}}{2} - \dfrac{{{c^2}}}{4}} \right)\\ \Leftrightarrow 9{a^2} = 4{a^2} + {b^2} + {c^2}\\\Leftrightarrow 5{a^2} = {b^2} + {c^2}.\end{array}\)
Advertisements (Quảng cáo)
Biến đổi đẳng thức \(\cot A = 2\left( {\cot B + \cot C} \right)\)
\( \Leftrightarrow \dfrac{{{b^2} + {c^2} - {a^2}}}{{abc}}R\)
\(= 2\left( {\dfrac{{{a^2} + {c^2} - {b^2}}}{{abc}}R + \dfrac{{{a^2} + {b^2} - {c^2}}}{{abc}}R} \right)\) ( theo bài 58).
\( \Leftrightarrow {b^2} + {c^2} = 5{a^2}\).
Vậy \(GB \bot GC\)
\(\Leftrightarrow \cot A = 2\left( {\cot B + \cot C} \right)\).
