Chứng minh rằng trong mỗi tam giác, khoảng cách d từ tâm đường tròn nội tiếp đến tâm đường tròn ngoại tiếp thỏa mãn hệ thức:
\({d^2} = {R^2} - 2Rr\). ( Hệ thức Ơ-le)
Giải
(h.58).
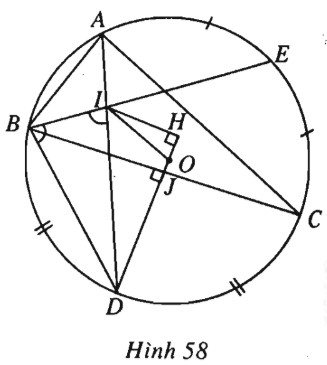
Xét tam giác \(ABC\) nội tiếp đường tròn \((O ; R)\) và ngoại tiếp đường tròn \((I ; r)\).
Gọi \(D, E\) lần lượt là điểm chính giữa cung \(\stackrel\frown {BC}\) và cung \(\stackrel\frown {AC}\) thì \(OD \bot BC , \widehat {BAD} = \dfrac{{\widehat A}}{2}\).
Mặt khác , ta có
\(\widehat {BID} = \dfrac{1}{2}\)(sđ\(\stackrel\frown {BD}\) +sđ \(\stackrel\frown {AE}\)) \)
\(= \dfrac{1}{2}\)(sđ \(\stackrel\frown {DC}\) + sđ \(\stackrel\frown {EC}\)) = \(\dfrac{1}{2}\)(sđ\(\stackrel\frown {DCE}\) ).
Advertisements (Quảng cáo)
Vậy \(\widehat {BID} = \widehat {IBD}\), suy ra \(ID = BD = 2R\sin \dfrac{A}{2}\).
Trong tam giác OID ta có \(O{I^2} = I{D^2} + O{D^2} - 2\overrightarrow {DI} .\overrightarrow {DO} \).\( \Rightarrow O{I^2} = 4R{\sin ^2}\dfrac{A}{2} + {R^2} - 2\overrightarrow {DO} .\overrightarrow {DH} \) (với \(IH \bot OD\)).
Dễ thấy
\(\overrightarrow {DO} .\overrightarrow {DH} = DO.(DJ + JH)\)
\(= R\left( {BD\sin \dfrac{A}{2} + r} \right) \)
\(= R\left( {2R{{\sin }^2}\dfrac{A}{2} + r} \right)\)
\(= 2{R^2}{\sin ^2}\dfrac{A}{2} + Rr\).
Từ đó suy ra \({d^2} = {R^2} - Rr\).
