Cho tam giác cân có cạnh bên bằng b nội tiếp trong đường tròn \((O ; R).\)
a) Tính cosin của các góc của tam giác.
b) Tính bán kính đường tròn nội tiếp tam giác.
c) Với giá trị nào của \(b\) thì tam giác đó có diện tích lớn nhất ?
Giải
(h.66)
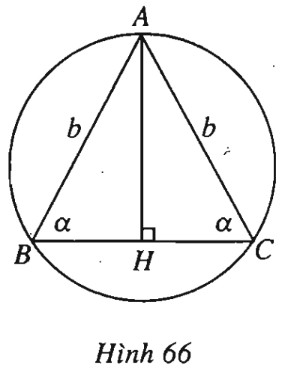
a) Giả sử tam giác đã cho là \(ABC\) có \(AB=AC=b.\)
Đặt \(\widehat B = \widehat C = \alpha \) thì \(\alpha < {90^0}\).
Ta có \(\sin \alpha = \dfrac{b}{{2R}}\) nên \(\cos B = \cos C = \sqrt {1 - \dfrac{{{b^2}}}{{4{R^2}}}} \)\( = \dfrac{{\sqrt {4{R^2} - {b^2}} }}{{2R}}\).
Ta lại có
Advertisements (Quảng cáo)
\(\begin{array}{l}\cos A = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}\\ = \dfrac{{2{b^2} - 4{b^2}{{\cos }^2}\alpha }}{{2{b^2}}}\\= 1 - 2{\cos ^2}\alpha \\ = 1 - 2\left( {1 - \dfrac{{{b^2}}}{{4{R^2}}}} \right) \\= \dfrac{{{b^2} - 2{R^2}}}{{2{R^2}}}.\end{array}\)
b) Diện tích tam giác là
\(S = \dfrac{1}{2}BC.AH = \dfrac{1}{2}2b\cos \alpha .b\sin \alpha \)
\(= {b^2}\cos \alpha \sin \alpha = \dfrac{{{b^3}\sqrt {4{R^2} - {b^2}} }}{{4{R^2}}}\).
Chu vi tam giác là \(2p = 2b + 2b\dfrac{{\sqrt {4{R^2} - {b^2}} }}{{2R}}\).
Bán kính đường tròn nội tiếp tam giác là \(r = \dfrac{S}{p} = \dfrac{{{b^2}\sqrt {4{R^2} - {b^2}} }}{{2R\left( {2R + \sqrt {4{R^2} - {b^2}} } \right)}}\).
c) Ta phải tìm \(b\) để \(y = {b^3}\sqrt {4{R^2} - {b^2}} \) đạt giá trị lớn nhất.
Viết lại \(y = 3\sqrt 3 \sqrt {\dfrac{{{b^2}}}{3}.\dfrac{{{b^2}}}{3}.\dfrac{{{b^2}}}{3}\left( {4{R^2} - {b^2}} \right)} \). Khi đó coi biểu thức trong căn là tích của bốn thừa số mà tổng của chúng bằng \(4{R^2}\) không đổi nên y đạt giá trị lớn nhất khi và chỉ khi \(\dfrac{{{b^2}}}{3} = 4{R^2} - {b^2}\) hay \(b = R\sqrt 3 \).
Khi đó \(\sin \alpha = \dfrac{{R\sqrt 3 }}{{2R}} = \dfrac{{\sqrt 3 }}{2} \Rightarrow \alpha = {60^0}\), ta được tam giác \(ABC\) là tam gác đều.
