Trong không gian Oxyz cho bốn điểm A(1;1;0), B(0;2;1), C(1;0;2), D(1;1;1).
a) Chứng minh bốn điểm đó không đồng phẳng. Tính thể tích tứ diện ABCD.
b) Tìm tọa độ trọng tâm của tam giác ABC, trọng tâm của tứ diện ABCD.
c) Tính diện tích các mặt của tứ diện ABCD.
d) Tính độ dài các đường cao của tứ diện ABCD.
e) Tính góc giữa hai đường thẳng AB và CD.
g) Viết phương trình mặt cầu ngoại tiếp tứ diện ABCD.

a) \(\overrightarrow {AB} = ( - 1;1;1),\overrightarrow {AC} = (0; - 1;2),\overrightarrow {AD} = (0;0;1)\)
Ta có : \(\left[ {\overrightarrow {AB} .\overrightarrow {AC} } \right].\overrightarrow {AD} = 1 \ne 0 \Rightarrow \overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) không đồng phẳng. Do đó bốn điểm A, B, C, D không đồng phẳng và
\({V_{ABCD}} = {1 \over 6}\left| {\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AD} } \right| = {1 \over 6}.\)
b) Gọi G là trọng tâm của tam giác ABC thì \(G = \left( {{2 \over 3};1;1} \right)\)
Gọi G’ là trọng tâm của tứ diện ABCD thì \(G’ = \left( {{3 \over 4};1;1} \right)\)
c) \({S_{ABC}} = {1 \over 2}\left| {\left[ {\overrightarrow {AB} .\overrightarrow {AC} } \right]} \right| \)
Advertisements (Quảng cáo)
\(= {1 \over 2}\sqrt {\left| \matrix{ 1 \hfill \cr - 1 \hfill \cr} \right.{{\left. \matrix{ 1 \hfill \cr 1 \hfill \cr} \right|}^2} + \left| \matrix{ 1 \hfill \cr 2 \hfill \cr} \right.{{\left. \matrix{ - 1 \hfill \cr 0 \hfill \cr} \right|}^2} + \left| \matrix{ - 1 \hfill \cr 0 \hfill \cr} \right.{{\left. \matrix{ 1 \hfill \cr - 1 \hfill \cr} \right|}^2}} = {{\sqrt {14} } \over 2}\)
\(\eqalign{ & {S_{ACD}} = {1 \over 2}\left| {\left[ {\overrightarrow {AC} ,\overrightarrow {AD} } \right]} \right|\cr& = {1 \over 2}\sqrt {\left| \matrix{ - 1 \hfill \cr 0 \hfill \cr} \right.{{\left. \matrix{ 2 \hfill \cr 1 \hfill \cr} \right|}^2} + \left| \matrix{ 2 \hfill \cr 1 \hfill \cr} \right.{{\left. \matrix{ 0 \hfill \cr 0 \hfill \cr} \right|}^2} + \left| \matrix{ 0 \hfill \cr 0 \hfill \cr} \right.{{\left. \matrix{ - 1 \hfill \cr 0 \hfill \cr} \right|}^2}} = {1 \over 2}. \cr & {S_{ADB}} = {1 \over 2}\left| {\left[ {\overrightarrow {AD} ,\overrightarrow {AB} } \right]} \right| \cr&= {1 \over 2}\sqrt {\left| \matrix{ 0 \hfill \cr 1 \hfill \cr} \right.{{\left. \matrix{ 1 \hfill \cr 1 \hfill \cr} \right|}^2} + \left| \matrix{ 1 \hfill \cr 1 \hfill \cr} \right.{{\left. \matrix{ 0 \hfill \cr - 1 \hfill \cr} \right|}^2} + \left| \matrix{ 0 \hfill \cr - 1 \hfill \cr} \right.{{\left. \matrix{ 0 \hfill \cr 1 \hfill \cr} \right|}^2}} = {{\sqrt 2 } \over 2}. \cr & {S_{BCD}} = {1 \over 2}\left| {\left[ {\overrightarrow {BC} ,\overrightarrow {BD} } \right]} \right| \cr&= {1 \over 2}\sqrt {\left| \matrix{ - 2 \hfill \cr - 1 \hfill \cr} \right.{{\left. \matrix{ 1 \hfill \cr 0 \hfill \cr} \right|}^2} + \left| \matrix{ 1 \hfill \cr 0 \hfill \cr} \right.{{\left. \matrix{ 1 \hfill \cr 1 \hfill \cr} \right|}^2} + \left| \matrix{ 1 \hfill \cr 1 \hfill \cr} \right.{{\left. \matrix{ - 2 \hfill \cr - 1 \hfill \cr} \right|}^2}} = {{\sqrt 3 } \over 2}. \cr} \)
d) Từ công thức tính thể tích khối tứ diện \(V = {1 \over 3}Bh\) (B là diện tích đáy,hlaf chiều cao tương ứng ) ta suy ra \(h = {{3V} \over B}.\)
Vậy nếu gọi \({h_A},{h_B},{h_C},{h_D}\) lần lượt là chiều cao hạ từ đỉnh A, B,C, D thì ta có :
\(\eqalign{ & {h_A} = {{3V} \over {{S_{BCD}}}} = {{3.{1 \over 6}} \over {{{\sqrt 3 } \over 2}}} = {1 \over {\sqrt 3 }},\cr&{h_B} = {{3V} \over {{S_{ACD}}}} = {{3.{1 \over 6}} \over {{1 \over 2}}} = 1. \cr & {h_C} = {{3V} \over {{S_{ABD}}}} = {{3.{1 \over 6}} \over {{{\sqrt 2 } \over 2}}} = {1 \over {\sqrt 2 }},\cr&{h_D} = {{3V} \over {{S_{ABC}}}} = {{3.{1 \over 6}} \over {{{\sqrt {14} } \over 2}}} = {1 \over {\sqrt {14} }}. \cr} \)
e) Vì \(\overrightarrow {AB} = ( - 1;1;1),\overrightarrow {CD} = (0;1; - 1)\) nên \(\overrightarrow {AB} .\overrightarrow {CD} = 0\), suy ra góc giữa AB và CD bằng 900.
g) Gọi I(x;y;z) là tâm mặt cầu ngoại tiếp tứ diện ABCD. Khi đó, ta có
\( \left\{ \matrix{ I{A^2} = I{B^2} \hfill \cr I{A^2} = I{C^2} \hfill \cr I{A^2} = ID \hfill \cr} \right.\)
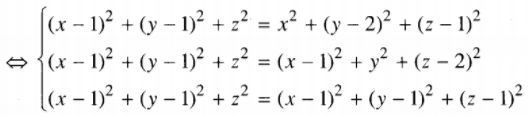
\( \Leftrightarrow \left\{ \matrix{ - 2x + 2y + 2z = 3 \hfill \cr - 2y + 4z = 3 \hfill \cr 2z = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x = - {3 \over 2} \hfill \cr y = - {1 \over 2} \hfill \cr z = {1 \over 2}. \hfill \cr} \right. \)
Vậy tâm của mặt cầu ngoại tiếp tứ giác ABCD là \(I\left( { - {3 \over 2}; - {1 \over 2};{1 \over 2}} \right)\) và bán kính của mặt cầu đó là
\(R = ID = \sqrt {{{\left( {{5 \over 2}} \right)}^2} + {{\left( {{3 \over 2}} \right)}^2} + {{\left( {{1 \over 2}} \right)}^2}} = {{\sqrt {35} } \over 2}.\)
Do đó, phương trình mặt cầu ngoại tiếp tứ diện ABCD là
\({\left( {x + {3 \over 2}} \right)^2} + {\left( {y + {1 \over 2}} \right)^2} + {\left( {z - {1 \over 2}} \right)^2} = {{35} \over 4}.\)
