Trong không gian Oxyz cho ba điểm A(1;0;0), B(0;0;1) và C(2;1;1).
a) Chứng minh A, B, C là ba đỉnh của một tam giác .
b) Tính chu vi, diện tích tam giác ABC.
c) Tìm tọa độ điểm D để ABCD là hình bình hành.
d) Tính độ dài đường cao \({h_A}\) của tam giác ABC kẻ từ A.
e) Tính các góc của tam giác ABC.
g) Xác định tọa độ trực tâm tam giác ABC.
h) Xác định tọa độ tâm đường tròn ngoại tiếp tam giác ABC.

a) Ta có \(\overrightarrow {CA} = ( - 1; - 1; - 1),\overrightarrow {CB} = ( - 2; - 1;0)\)
\( \left[ {\overrightarrow {CA} ,\overrightarrow {CB} } \right] = \left( {\left| \matrix{ - 1 \hfill \cr - 1 \hfill \cr} \right.\left. \matrix{ - 1 \hfill \cr 0 \hfill \cr} \right|;\left| \matrix{ - 1 \hfill \cr 0 \hfill \cr} \right.\left. \matrix{ - 1 \hfill \cr - 2 \hfill \cr} \right|;\left| \matrix{ - 1 \hfill \cr - 2 \hfill \cr} \right.\left. \matrix{ - 1 \hfill \cr - 1 \hfill \cr} \right|} \right) \)
\(= ( - 1;2; - 1) \ne \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {CA} ,\overrightarrow {CB} \) không cùng phương hay A, B, C không thẳng hàng, tức A, B, C là ba đỉnh của một tam giác.
b) Chu vi tam giác ABC bằng \(AB + BC + CA = \sqrt 2 + \sqrt 5 + \sqrt 3 \)
\({S_{ABC}} = {1 \over 2}\left| {\left[ {\overrightarrow {CA} ,\overrightarrow {CB} } \right]} \right| \)
\(= {1 \over 2}\sqrt {{{( - 1)}^2} + {2^2} + {{( - 1)}^2}} = {{\sqrt 6 } \over 2}.\)
c) Giả sử D = (x,y,z) ta có : \(\overrightarrow {AB} = ( - 1;0;1),\overrightarrow {DC} = (2 - x;1 - y;1 - z).\)
Tứ giác ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \matrix{ 2 - x = - 1 \hfill \cr 1 - y = 0 \hfill \cr 1 - z = 1 \hfill \cr} \right. \Rightarrow D = (3;1;0).\)
d) Gọi \({h_A}\) là đường cao của tam giác ABC kẻ từ A, ta có :
\({h_A} = {{2{S_{ABC}}} \over {BC}} = {{\sqrt 6 } \over {\sqrt 5 }} = {{\sqrt {30} } \over 5}\)
Advertisements (Quảng cáo)
e) \({\mathop{\rm cosA}\nolimits} = {{\overrightarrow {AB} .\overrightarrow {AC} } \over {\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = 0 \Rightarrow A = {90^0}\) (tam giác ABC vuông tại A).
\(\eqalign{ & \cos B = {{\overrightarrow {BA} .\overrightarrow {BC} } \over {\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}} = {2 \over {\sqrt {10} }} = {{\sqrt {10} } \over 5}. \cr & \cos C = {{\overrightarrow {CA} .\overrightarrow {CB} } \over {\left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|}} = {3 \over {\sqrt {15} }} = {{\sqrt {15} } \over 5}. \cr} \)
g) Tam giác ABC vuông tại A nên trực tâm H trùng A. Vậy H=(1;0;0).
Ta có thể làm cách khác như sau :
Gọi H(x;y;z) là trực tâm của tam giác ABC, ta có hệ
\(\eqalign{ & \left\{ \matrix{ \overrightarrow {AH} .\overrightarrow {BC} = 0 \hfill \cr \overrightarrow {BH} .\overrightarrow {AC} = 0 \hfill \cr \overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AH} \text{ đồng phẳng}\hfill \cr} \right. \cr & \cr} \)
\( \Leftrightarrow \left\{ \matrix{ \overrightarrow {AH} .\overrightarrow {BC} = 0 \hfill \cr \overrightarrow {BH} .\overrightarrow {AC} = 0 \hfill \cr \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AH} = 0. \hfill \cr} \right.\)
Ta có :
\(\eqalign{ & \overrightarrow {AH} = (x - 1;y;z),\overrightarrow {BC} = (2;1;0),\cr&\overrightarrow {BH} = (x;y;z - 1), \cr & \overrightarrow {AB} = ( - 1;0;1),\overrightarrow {AC} = (1;1;1) \cr & \Rightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = ( - 1;2; - 1),\cr&\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AH} = 1 - x + 2y - z. \cr} \)
Vậy ta có hệ phương trình :
\(\left\{ \matrix{ 2x - 2 + y = 0 \hfill \cr x + y + z - 1 = 0 \hfill \cr 1 - x + 2y - z = 0 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ 2x + y = 2 \hfill \cr x + y + z = 1 \hfill \cr x - 2y + z = 1 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x = 1 \hfill \cr y = 0 \hfill \cr z = 0 \hfill \cr} \right. \Rightarrow H(1;0;0).\)
h) Tam giác ABC vuông tại A nên tâm I của đường tròn ngoại tiếp tam giác là trung điểm của cạnh huyền BC. Do đó \(I = \left( {1;{1 \over 2};1} \right).\)
Ta có thể làm cách như sau:
Gọi I(x;y;z) là tâm đường tròn ngoại tiếp \(\Delta ABC\). Ta có hệ
\(\left\{ \matrix{ AI = BI \hfill \cr AI = CI \hfill \cr\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AI} \text{ đồng phẳng} \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \matrix{ A{I^2} = B{I^2} \hfill \cr A{I^2} = C{I^2} \hfill \cr \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AI} = 0 \hfill \cr} \right. \)
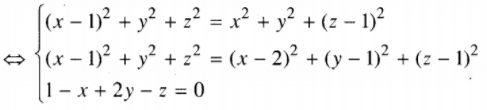
\( \Leftrightarrow \left\{ \matrix{ x = 1 \hfill \cr y = {1 \over 2} \hfill \cr z = 1 \hfill \cr} \right. \Rightarrow I(1;{1 \over 2};1). \)
