Cho khối chóp tam giác đều . Bài 33 trang 10 Sách bài tập Hình học lớp 12 Nâng cao - Bài 4. Thể tích của khối đa diện
Cho khối chóp tam giác đều \(S.ABC\) có chiều cao bằng h và góc ASB bằng \(2\varphi \). Hãy tính thể tích khối chóp.
(h.17)
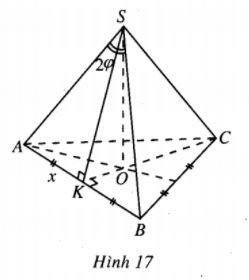
Giả sử O là tâm của tam giác đều ABC.
Advertisements (Quảng cáo)
Khi đó \(SO \bot \left( {ABC} \right)\) và SO = h.
Gọi K là trung điểm của AB. Đặt AK = x.
Khi đó \(\eqalign{ & SK = x\cot \varphi ;\;OK = xtan{30^0} = {x \over {\sqrt 3 }}. \cr & {h^2} = S{K^2} - O{K^2} = {{{x^2}} \over 3}(3{\cot ^2}\varphi - 1) \cr & \Rightarrow {x^2} = {{3{h^2}} \over {3{{\cot }^2}\varphi - 1}}. \cr} \)
Ta có: \(\eqalign{ & {S_{ABC}} = {{A{B^2}\sin {{60}^0}} \over 2} = {x^2}\sqrt 3 , \cr & \Rightarrow {V_{S.ABC}} = {1 \over 3}{S_{ABC}}.h = {{{x^2}\sqrt 3 } \over 3}h = {{{h^3}\sqrt 3 } \over {3{{\cot }^2}\varphi - 1}}. \cr} \)