Khối chóp \(S.ABCD\)có \(SA \bot \left( {ABC} \right)\); đáy là tam giác ABC cân tại A, độ dài trung tuyến AD bằng a, cạnh bên SB tạo với đáy một góc \( \alpha \) và tạo với mặt \(\left( {SAD} \right)\) góc \(\beta \). Tính thể tích khối chóp.

(h.20)
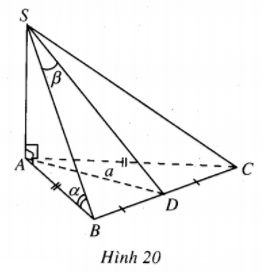
AB là hình chiếu của SB trên \(mp\left( {ABC} \right)\) nên \(\widehat {SBA} = \alpha \) Dễ thấy \(BD \bot \left( {SAD} \right)\) nên hình chiếu của SB trên \(mp\left( {SAD} \right)\) là SD \( \Rightarrow \) \(\widehat {BSD} = \beta \)
Advertisements (Quảng cáo)
Do SAB và SDB là các tam giác vuông nên ta có \(SB = {{BD} \over {\sin \beta }},SB = {{AB} \over {\cos \alpha }},\) suy ra
\(\eqalign{ &{{A{B^2}} \over {{{\cos }^2}\alpha }} = {{B{D^2}} \over {{{\sin }^2}\beta }} = {{A{B^2} - B{D^2}} \over {{{\cos }^2}\alpha - {{\sin }^2}\beta }} \cr&= {{{a^2}} \over {{{\cos }^2}\alpha - {{\sin }^2}\beta }} \cr & \Rightarrow BD = {{a\sin \beta } \over {\sqrt {{{\cos }^2}\alpha - {{\sin }^2}\beta } }}, \cr} \)
\(\eqalign{ & SD = BD\cot \beta = {{a\cos \beta } \over {\sqrt {{\rm{co}}{{\rm{s}}^2}\alpha - {{\sin }^2}\beta } }}, \cr & SA = \sqrt {S{D^2} - A{D^2}} = {{a\sin \alpha } \over {\sqrt {{\rm{co}}{{\rm{s}}^2}\alpha - {{\sin }^2}\beta } }}. \cr & \cr} \)
Vậy :
\(\eqalign{ & {V_{S.ABC}} = {1 \over 3}{S_{ABC}}.SA \cr & = {1 \over 3}.a.{{a\sin \beta } \over {\sqrt {{\rm{co}}{{\rm{s}}^2}\alpha - {{\sin }^2}\beta } }}.{{a\sin \alpha } \over {\sqrt {{\rm{co}}{{\rm{s}}^2}\alpha - {{\sin }^2}\beta } }} \cr & = {{{a^3}\sin \alpha .\sin \beta } \over {3\left( {{\rm{co}}{{\rm{s}}^2}\alpha - {{\sin }^2}\beta } \right)}}. \cr} \)
