Cho khối lăng trụ tam giác \(ABC.A’B’C’\) có cạnh đáy bằng a, chiều cao bằng h. Tính thể tích khối chóp A.BC’A’.

(h.26) Cách 1.
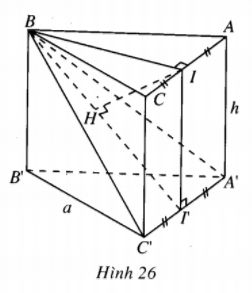
\(AC//A’C’ \Rightarrow AC//\left( {BC’A’} \right).\) Gọi I là trung điểm của AC thì
\(d\left( {A,\left( {BC’A’} \right)} \right) = d\left( {I,\left( {BC’A’} \right)} \right).\)
Gọi I’ là trung điểm của A’C’ thì rõ ràng \(BI’ \bot A’C’,\) mặt khác \(II’ \bot A’C’\) nên \(A’C’ \bot \left( {IBI’} \right).\)
Vậy khi ta hạ \(IH \bot BI’\) thì \(A’C’ \bot IH.\)
Advertisements (Quảng cáo)
Từ đó suy ra \(IH \bot \left( {BC’A’} \right),\) tức là \(d\left( {A,\left( {BC’A’} \right)} \right) = IH.\)
Ta có :
\(\eqalign{ & IH = {{IB.II’} \over {BI’}} = {{a.{{\sqrt 3 } \over 2}.h} \over {\sqrt {3.{{{a^2}} \over 4} + {h^2}} }} = {{\sqrt 3 ah} \over {\sqrt {3{a^2} + 4{h^2}} }}, \cr & {S_{BC’A’}} = {1 \over 2}BI’.C’A’ = {1 \over 2}\sqrt {{{3{a^2}} \over 4} + {h^2}} .a \cr&\;\;\;\;\;\;\;\;\;\;\;= {1 \over 4}a\sqrt {3{a^2} + 4{h^2}} . \cr} \)
Vậy
\({V_{A.BC’A’}} = {1 \over 3}.{1 \over 4}.a.\sqrt {3{a^2} + 4{h^2}} .{{\sqrt 3 ah} \over {\sqrt {3{a^2} + 4{h^2}} }} = {{\sqrt 3 {a^2}h} \over {12}}\)
Cách 2.
\(\eqalign{ {V_{A.BC’A’}} = {V_{B.AA’C’}}& = {1 \over 2}.{V_{B.AA’C’C}} \cr&= {1 \over 2}.{2 \over 3}.{V_{ABC.A’B’C’}} \cr & = {1 \over 3}.{S_{ABC}}.h\cr& = {1 \over 3}.{{{a^2}\sqrt 3 } \over 4}.h = {{{a^2}\sqrt 3 } \over {12}}.h \cr} \)
