Khối chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm của AB, AD và SC. Chứng minh mặt phẳng \(\left( {MNP} \right)\) chia khối chóp thành hai phần có thể tích bằng nhau.

(h.29).
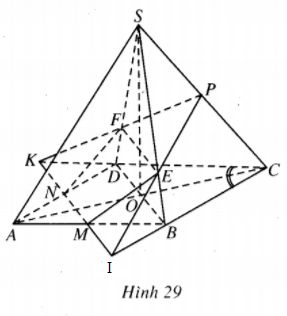
Giả sử đường thẳng MN cắt CD và BC lần lượt tại K và I.
Dễ thấy :
\(\eqalign{ & CK = {3 \over 2}CD,CI = {3 \over 2}CB, \cr & d\left( {P,\left( {ABC} \right)} \right) = {1 \over 2}d\left( {S,\left( {ABC} \right)} \right). \cr & \cr} \)
\({V_{P.CIK}} = {1 \over 3}.{1 \over 2}CI.CK\sin \widehat {ICK} \) .\(d\left( {P,\left( {ABC} \right)} \right)\)
\( = {1 \over 3}.{1 \over 2}.{3 \over 2}CB.{3 \over 2}CD\sin \widehat {BCD} \) .\({1 \over 2}d\left( {S,(ABC)} \right)\)
Advertisements (Quảng cáo)
=\({9 \over {16}}({1 \over 3}CB.CD\sin \widehat {BCD} \) .\(d\left( {S,({\rm{ABC)}}} \right)\)
\( \Rightarrow {V_{P.CIK}} = {9 \over {16}}{V_{S.ABCD}}.\)
Ta có :
\(\eqalign{ & {{{V_{I.BEM}}} \over {{V_{I.CPK}}}} = {{IB} \over {IC}}.{{IE} \over {IP}}.{{IM} \over {IK}} = {1 \over 3}.{1 \over 2}.{1 \over 3} = {1 \over {18}} \cr & \Rightarrow {V_{I.BEM}} = {1 \over {18}}{V_{I.CPK}} = {1 \over {18}}{V_{P.CIK}} \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= {1 \over {32}}{V_{S.ABCD}}. \cr} \)
Tương tự , ta cũng có \({V_{K.NDF}} = {1 \over {18}}{V_{P.CIK}} = {1 \over {32}}{V_{S.ABCD}}.\)
Vậy nếu gọi V2 là thể tích của phần khối chóp giới hạn bởi \(mp\left( {MNP} \right)\) với mặt phẳng đáy thì :
\(\eqalign{ & {V_2} = {V_{P.CIK}} - \left( {{V_{I.BEM}} + {V_{K.NDF}}} \right) \cr & = {9 \over {16}}{V_{S.ABCD}} - \left( {{1 \over {32}}{V_{S.ABCD}} + {1 \over {32}}{V_{S.ABCD}}} \right) \cr & = {9 \over {16}}{V_{S.ABCD}} - {1 \over {16}}{V_{S.ABCD}} = {1 \over 2}{V_{S.ABCD}}. \cr} \)
Vậy phần còn lại, tức là phần của khối chóp nằm trên \(mp\left( {MNP} \right)\), có thể tích V1 cũng bằng \({1 \over 2}{V_{S.ABCD}}\).
Do đó V1 = V2.
