Khối chóp S.ABCD có đáy là hình bình hành. Gọi B’, D’ lần lượt là trung điểm của SB, SD. Mặt phẳng \(\left( {AB’D’} \right)\) cắt SC tại C’. Tìm tỉ số thể tích của hai khối chóp S.AB’C’D’ và S.ABCD.

(h.28)
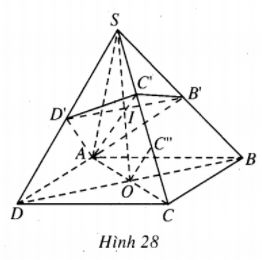
Dễ thấy \(AC’,B’D’\) và \(SO\left( {O = AC \cap BD} \right)\) đồng quy tại \(I\) và \(I\) là trung điểm của SO.
Kẻ \(OC”//AC’.\) Dễ thấy \(SC’ = C’C” = C”C.\)
Advertisements (Quảng cáo)
Vậy \({{SC’} \over {SC}} = {1 \over 3}.\) Ta có
\(\eqalign{ & {{{V_{S.AB’C’}}} \over {{V_{S.ABC}}}} = {{SB’} \over {SB}}.{{SC’} \over {SC}} = {1 \over 2}.{1 \over 3} = {1 \over 6} \cr & \Rightarrow {{{V_{S.AB’C’}}} \over {{V_{S.ABCD}}}} = {1 \over {12}}. \cr} \)
Chứng minh tương tự, ta cũng có :
\({{{V_{S.AC’D’}}} \over {{V_{S.ABCD}}}} = {1 \over {12}}.\)
Vậy \({{{V_{S.AB’C’D’}}} \over {{V_{S.ABCD}}}} = {{{V_{S.AB’C’}} + {V_{S.AC’D’}}} \over {{V_{S.ABCD}}}} = {1 \over 6}.\)
