. Câu 1 trang 209 sách bài tập Giải tích 12 Nâng cao – Ôn tập cuối năm Giải tích
Advertisements (Quảng cáo)
Cho hàm số:
\(f\left( x \right) = 1 + x + {{{x^2}} \over 2} – {e^x}\)
a) Chứng minh rằng \(f’\left( x \right) < 0\) với mọi x < 0
b) Chứng minh bất đẳng thức
\(1 + x < {e^x} + x + {{{x^2}} \over 2}\) với mọi x < 0
Hướng dẫn:
a) \(f’\left( x \right) = 1 + x – {e^x},f”\left( x \right) = 1 – {e^x}\)
\(f”\left( x \right) = 0 \Leftrightarrow x = 0\)
Advertisements (Quảng cáo)
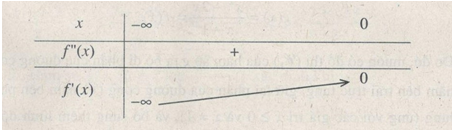
Dựa vào bảng biến thiên, ta có \(f’\left( x \right) > 0\) với mọi x < 0.
b) Từ a) suy ra f nghịch biến trên nửa khoảng\(\left( { – \infty ;0} \right]\). Do đó
\(f(x) > f(0)\) , với mọi x < 0,
Hay \(1 + x + {{{x^2}} \over 2} – {e^x} > 0\) với mọi x < 0
c) Từ b) suy ra
\(1 – 0,01 < {e^{ – 0,01}} < 1 – 0,01 + {{0,0001} \over 2}\) .