Bài tập - Chủ đề 4: Tam giác cân. Định lý Pythagore - Bài 12 trang 169 Tài liệu dạy – học Toán 7 tập 1. Giải bài tập Lần lượt tính độ dài các cạnh huyền a, b, c, d của các tam giác vuông theo hình 19. Hãy dự đoán kết quả của các cạnh huyền còn lại.
Lần lượt tính độ dài các cạnh huyền a, b, c, d của các tam giác vuông theo hình 19. Hãy dự đoán kết quả của các cạnh huyền còn lại.
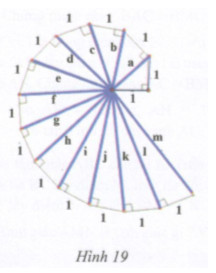
Áp dụng định lý Pythagore cho tam giác vuông, ta có:
\({a^2} = {1^2} + {1^2} = 2.\) Mà a > 0 do đó: \(b = \sqrt 2 .\)
Advertisements (Quảng cáo)
\({b^2} = {1^2} + {a^2} = 1 + 2 = 3.\) . Mà b > 0 do đó \(b = \sqrt 3 .\)
\({c^2} = {b^2} + 1 = 3 + 1 = 4.\) Mà c > 0 do đó: \(c = \sqrt 4 = 2.\)
\({d^2} = {c^2} + {1^2} = 4 + 1 = 5.\) Mà d > 0 do đó: \(d = \sqrt 5 .\)
Dự đoán độ dài các cạnh huyền còn lại lần lượt là:
\(\eqalign{ & e = \sqrt 6 ,f = \sqrt 7 ,g = \sqrt 8 ,h = \sqrt 9 = 3 \cr & i = \sqrt {10} ,j = \sqrt {11} ,k = \sqrt {12} \cr & l = \sqrt {13} ,m = \sqrt {14} \cr} \)