
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Kẻ \(HF \bot AB,HF \bot AC(E \in AB,F \in AC).\) Chứng minh rằng AE = AF.
b) Chứng minh rằng EF // BC.

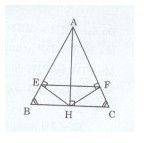
a)Tam giác ABC cân tại A (gt) => AB = AC và \(\widehat {ABC} = \widehat {ACB}.\)
Mà \(\widehat {ABH} + \widehat {BAH} = {90^0}(\Delta ABH\) vuông tại H)
Và \(\widehat {ACH} + \widehat {CAH} = {90^0}(\Delta ACH\) vuông tại H).
Nên \(\widehat {BAH} = \widehat {CAH}.\)
Xét tam giác AEH vuông tại E \((HE \bot AB)\)
Và tam giác AFH vuông tại F \((HF \bot AC)\) có:
Advertisements (Quảng cáo)
AH là cạnh chung.
\(\widehat {EAH} = \widehat {FAH}\) (chứng minh trên).
Do đó: \(\Delta AEH = \Delta AFH\) (cạnh huyền - góc nhọn) => AE = AF.
b)Tam giác AEF có: AE = AF => tam giác AEF cân tại A\(\widehat {AEF} = \widehat {AFE}.\)
Mà \(\widehat {AEF} + \widehat {AFE} + \widehat {EAF} = {180^0}\) (tổng ba góc của một tam giác).
Nên \(\widehat {AEF} + \widehat {AEF} + \widehat {EAF} = {180^0} \to 2\widehat {AEF} + \widehat {EAF} = {180^0} \Rightarrow \widehat {AEF} = {{{{180}^0} - \widehat {EAF}} \over 2}(1)\)
Tam giác ABC có: \(\widehat {ABC} + \widehat {BAC} + \widehat {ACB} = {180^0}\) mà \(\widehat {ABC} = \widehat {ACB}(\Delta ABC\) cân tại A)
Nên \(\widehat {ABC} + \widehat {ABC} + \widehat {BAC} = {180^0} \Rightarrow 2\widehat {ABC} + \widehat {BAC} = {180^0} \Rightarrow \widehat {ABC} = {{{{180}^0} - \widehat {BAC}} \over 2}(2)\)
Từ (1) và (2) suy ra: \(\widehat {AEF} = \widehat {ABC}.\)
Mà góc AEF và ABC đồng vị. Do đó EF // BC.
