
Cho tam giác MNP vuông tại M. Tia phân giác của góc N cắt MP tại E. Kẻ \(EF \bot NP(F \in NP).\)
a) Chứng minh rằng tam giác MNF cân.
b) Kẻ \(MH \bot NP.\) Chứng minh rằng MF là phân giác của góc HME.

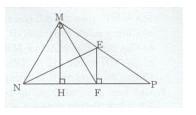
a)Xét tam giác MNE vuông tại M và tam giác NEF vuông tại F ta có:
\(\widehat {MNE} = \widehat {FNE}\) (NE là tia phân giác của góc MNF)
NE là cạnh chung.
Advertisements (Quảng cáo)
Do đó: \(\Delta MNE = \Delta FNE\) (cạnh huyền - góc nhọn)
=>MN = NF => tam giác MNF cân tại N.
b) Ta có: \(ME = EF(\Delta MNE = \Delta FNE)\)
=>Tam giác MEF cân tại E \(\Rightarrow \widehat {EMF} = \widehat {EFM}\)
Mặt khác \(MH \bot NP(gt);EF \bot NP(gt)\)
\(\Rightarrow MH//EF \Rightarrow \widehat {HMF} = \widehat {EFM}\) (hai góc so le trong).
Mà \(\widehat {EMF} = \widehat {EFM}(cmt) \Rightarrow \widehat {HMF} = \widehat {EMF}\)
Vậy MF là tia phân giác của góc HME.
