. Câu 54 trang 166 Sách bài tập (SBT) Toán 8 tập 1 - Ôn tập chương II - Đa giác - Diện tích đa giác
Tam giác ABC có hai trung tuyến AM và BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo AM và BN
Giải:
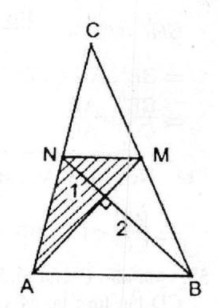
Tứ giác ABMN có hai đường chéo vuông góc.
\({S_{ABMN}} = {1 \over 2}AM.BN\)
Advertisements (Quảng cáo)
∆ ABM và ∆ AMC có chung chiều cao kẻ từ A cạnh đáy BM = MC
\( \Rightarrow {S_{ABM}} = {S_{AMC}} = {1 \over 2}{S_{ABC}}\)
∆ MAN và ∆ MNC có chung chiều cao kẻ từ M, cạnh đáy AN = NC
\(\eqalign{ & \Rightarrow {S_{MAN}} = {S_{MNC}} = {1 \over 2}{S_{AMC}} = {1 \over 4}{S_{ABC}} \cr & {S_{ABMN}} = {S_{ABM}} + {S_{MNA}} = {1 \over 2}{S_{ABC}} + {1 \over 4}{S_{ABC}} = {3 \over 4}{S_{ABC}} \cr & \Rightarrow {S_{ABC}} = {4 \over 3}{S_{ABMN}} = {4 \over 3}.{1 \over 2}.AM.BN = {2 \over 3}AM.BN \cr} \)
