
Cho tam giác ABC (AB < AC). Gọi M, N lần lượt là trung điểm của BC và AC.
a) Tứ giác ABMN là hình gì ? Vì sao ?
b) Gọi E là điểm đối xứng của M qua N. Chứng minh rằng tứ giác AECM là hình bình hành.
c) Tam giác ABC cần có thêm điều kiện gì để tứ giác AECM lần lượt là:
- Hình chữ nhật
- Hình thoi
- Hình vuông.

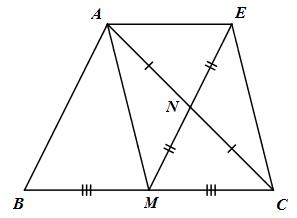
a) Gọi M, N lần lượt là trung điểm của BC và AC (gt) ;
\( \Rightarrow MN\) là đường trung bình của tam giác ABC
\( \Rightarrow MN//AC \Rightarrow \) Tứ giác MNAB là hình thang.
b) Tứ giác AECM có AC và ME cắt nhau tại N (gt)
N là trung điểm của AC (gt)
Advertisements (Quảng cáo)
N là trung điểm của ME (E đối xứng với M qua N)
Do đó tứ giác AECM là hình bình hành.
c) Ta có tứ giác AECM là hình bình hành.
* Tứ giác AECM là hình chữ nhật \( \Leftrightarrow \) Hình bình hành AECM có \(\widehat {AMC} = {90^0}\)
\( \Rightarrow \Delta ABC\) có AM là đường cao đồng thời là đường trung tuyến.
\( \Leftrightarrow \Delta ABC\) cân tại A.
Vậy tam giác ABC có thêm điều kiện là tam giác ABC cân tại A để tứ giác AEMC là hình chữ nhật.
* Tứ giác AECM là hình thoi \( \Leftrightarrow \) Hình bình hành AECM có \(AM = MC\).
\( \Rightarrow \Delta ABC\) có AM là đường trung tuyến, \(AM = {{BC} \over 2} \Leftrightarrow \Delta ABC\) vuông tại A.
Vậy tam giác ABC cần có thêm điều kiện là tam giác ABC vuông tại A để tứ giác AECM là hình thoi.
* Tứ giác AECM là hình vuông \( \Leftrightarrow \) Hình chữ nhật AECM có \(AM = MC \Leftrightarrow \Delta ABC\) cân tại A.
Hình chữ nhật AECM có thêm điều kiện \(\widehat {AMC} = {90^0}\)
\( \Leftrightarrow \Delta ABC\) vuông tại A.
Vậy tam ABC cần có thêm điều kiện là tam giác ABC vuông cân tại A để tứ giác AECM là hình vuông.
