
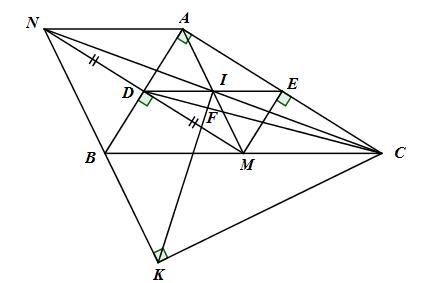
Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC. Vẽ \(MD \bot AB(D \in AB)\) và \(ME \bot AC(E \in AC)\) .
a) Chứng minh rằng tứ giác ADME là hình chữ nhật.
b) Trên tia đối của tia DM lấy điểm N sao cho D là trung điểm MN. Chứng minh rằng tứ giác AMBN là hình thoi.
c) AM cắt CD tại F. Chứng minh rằng \(MB = 3MF.\)
d) Gọi I là giao điểm hai đường chéo của hình chữ nhật ADME. Vẽ CK vuông góc với BN tại K. Chứng minh rằng tứ giác IKC cân.

a) Xét tứ giác ADME có: \(\widehat {ADE} = {90^0}\) (\(\Delta ABC\) vuông tại A)
\(\widehat {ADM} = {90^0}\) (\(MD \bot AB\) tại D) và \(\widehat {AEM} = {90^0}\) (\(ME \bot AC\) tại E)
Do đó tứ giác ADME là hình chữ nhật.
b) \(\Delta ABC\) có M là trung điểm của BC.
Và MD // AC (MD // AE, \(E \in AC\))
\( \Rightarrow D\) là trung điểm của AB.
Và D là trung điểm của NM (gt)
Do đó tứ giac AMBN là hình bình hành
Advertisements (Quảng cáo)
Mà \(AB \bot NM\,\,\left( {gt} \right)\) nên tứ giác AMBN là hình thoi.
c) \(\Delta ABC\) vuông tại A có AM là đường trung tuyến (M là trung điểm của BC)
\( \Rightarrow AM = {1 \over 2}BC\).
Mà \(BM = {1 \over 2}BC\) (M là trung điểm của BC) nên \(AM = BM\).
\(\Delta ABC\) có AM cắt CD tại F (gt);
AM là đường trung tuyến (M là trung điểm của BC)
CD là đường trung tuyến (D là trung điểm của AB)
\( \Rightarrow F\) là trọng tâm của tam giác ABC \( \Rightarrow FM = {1 \over 3}AM \Rightarrow AM = 3FM\).
Mà \(AM = BM\,\,\left( {cmt} \right) \Rightarrow BM = 3MF\).
d) Hình chữ nhật ADME có AM và DE cắt nhau tại I (gt) \( \Rightarrow I\) là trung điểm của AM.
Tứ giác ANMC có \(AN = MC\,\,\left( { = BM} \right)\) và AN // MC (AN //BM, \(M \in BC\))
\( \Rightarrow ANMC\) là hình bình hành \( \Rightarrow \) AM và NC cắt nhau tại trung điểm của mỗi đường.
Mà I là trung điểm của AM (cmt) nên I là trung điểm của NC.
\( \Rightarrow KI = IC = {1 \over 2}NC \Rightarrow \Delta IKC\) cân tại I.
