
Tam giác ABC có BC bằng 15 cm. Trên đường cao AH lấy các điểm K, I sao cho AK = KI = IH. Qua I và K kẻ các đường \(EF // BC, MN // BC.\)
a) Tính độ dài các đoạn thẳng MN và EF.
b) Tính diện tích tứ giác MNFE biết rằng diện tích tam giác ABC là 270 cm2.

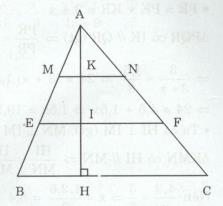
a) Ta có \(AH = AK + KI + IH\) và \(AK = KI = IH(gt) \)
\(\Rightarrow AH = 3AK \Rightarrow {{AK} \over {AH}} = {1 \over 3}\)
∆ABH có \(MK//BH(gt) \Rightarrow {{AM} \over {AB}} = {{AK} \over {AH}}\) (hệ quả của định lý Thales) \( \Rightarrow {{AM} \over {AB}} = {1 \over 3}\)
∆ABC có \(MN//BC(gt) \Rightarrow {{MN} \over {BC}} = {{AM} \over {AB}}\) (hệ quả của định lý Thales)
\( \Rightarrow {{MN} \over {BC}} = {1 \over 3}\)
\(\Rightarrow {{MN} \over {15}} = {1 \over 3}\)
\(\Rightarrow MN = {{15} \over 3} = 5(cm)\)
Advertisements (Quảng cáo)
∆AEI có MK // EI (gt)
Và K là trung điểm của AI (AK = KI)
=> M là trung điểm của AE
Xét ∆AEF có MN // EF (gt)
\( \Rightarrow {{MN} \over {EF}} = {{AM} \over {AE}}\) (hệ quả của định lý Thales)
Mà \({{AM} \over {AE}} = {1 \over 2}\) (M là trung điểm của AE)
Nên
\(\eqalign{ & {{MN} \over {EF}} = {1 \over 2}\cr& \Rightarrow {5 \over {EF}} = {1 \over 2} \cr&\Rightarrow EF = 10(cm) \cr & b)\;{S_{ABC}} = {1 \over 2}AH.BC\cr& \Rightarrow 270 = {1 \over 2}.AH.15 \cr&\Rightarrow AH = {{270.2} \over {15}} = 36(cm) \cr} \)
Ta có AH = 3AK (câu a) và AK = KI (gt)
Do đó \(AH = 3KI \)
\(\Rightarrow KI = \dfrac{AH}{ 3} = \dfrac{36}{3} = 12(cm)\)
\({S_{MNFE}} = \dfrac{1 }{ 2}KI(MN + EF) \)\(\,= \dfrac{1 }{2}.12(5 + 10) = 90(c{m^2})\)
