
Tìm x trong các hình vẽ sau:
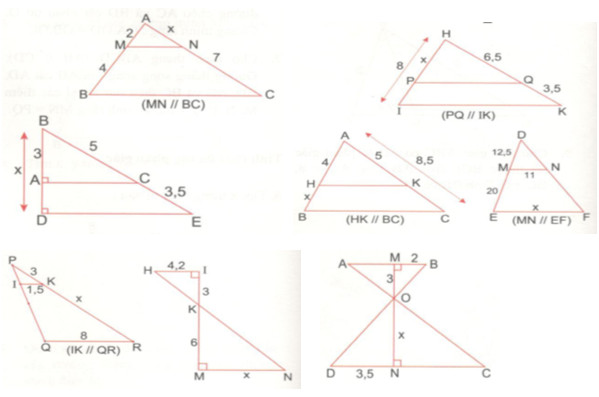

• ∆ABC có MN // BC (gt) \( \Rightarrow {{AN} \over {CN}} = {{AM} \over {BM}}\) (định lý Thales)
Nên \({x \over 7} = {2 \over 4} \Rightarrow x = {{2.7} \over 4} = 3,5\)
• Ta có \(CA \bot BD(gt)\) và \(DE \bot BD(gt) \Rightarrow CA//DE\)
\(BE = BC + CE = 5 + 3,5 = 8,5\)
∆BDE có DE // CA \( \Rightarrow {{BA} \over {BD}} = {{BC} \over {BE}}\) (định lý Thales)
\(\eqalign{ & \Rightarrow {3 \over x} = {5 \over {8,5}}\cr& \Rightarrow x = {{3.8,5} \over 5} = 5,1 \Leftrightarrow x = 5,1 \cr & CK = AC - AK = 8,5 - 5 = 3,5 \cr} \)
∆ABC có HK // BC \( \Rightarrow {{AH} \over {BH}} = {{AK} \over {CK}}\) (định lý Thales)
\( \Rightarrow {4 \over x} = {5 \over {3,5}}\)
\(\Rightarrow x = {{4.3,5} \over 7} = 2,8 \Leftrightarrow x = 2,8\)
• DE = DM + ME = 12,5 + 20 = 32,5
∆DEF có MN// EF (gt) \( \Rightarrow {{MN} \over {EF}} = {{DM} \over {DE}}\) (Hệ quả của định lí Thales)
\( \Rightarrow {{11} \over x} = {{12,5} \over {32,5}}\)
Advertisements (Quảng cáo)
\(\Rightarrow x = {{32,5.11} \over {12,5}} = 28,6 \Leftrightarrow x = 28,6\)
• PR = PK + KR = 3 + x
∆PQR có IK//QR (gt) \( \Rightarrow {{PK} \over {PR}} = {{IK} \over {QR}}\) (Hệ quả của định lí Thales)
\({3 \over {3 + x}} = {{1,5} \over 8} \Rightarrow 24 = (3 + x).1,5\)
\( \Rightarrow 24 = 4,5 + 1,5x \Rightarrow 1,5x = 19,5\)
\(\Rightarrow x = 13 \Leftrightarrow x = 13\)
• Ta có \(HI \bot IM(gt),MN \bot IM(gt)\)
\(\Rightarrow HI//MN\)
∆KMN có HI//MN \( \Rightarrow {{HI} \over {MN}} = {{IK} \over {MK}}\) (Hệ quả của định lí Thales)
Nên \({{4,2} \over x} = {3 \over 6} \Rightarrow x = {{4,2.6} \over 3} = 8,4\)
• Ta có \(MB \bot MN(gt),MN \bot IM(gt) \)
\(\Rightarrow HI//MN\)
∆ODN có MB//DN \( \Rightarrow {{OM} \over {ON}} = {{MB} \over {ND}}\) (Hệ quả của định lí Thales)
Nên \({3 \over x} = {3 \over {3,5}} \Rightarrow x = {{3.3,5} \over 2} = 5,25\)
