
Tam giác ABC có đường cao AH. Đường thẳng d // BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B’, C’ và H’ (xem hình vẽ).
a) Chứng minh rằng: \({{AH’} \over {AH}} = {{B’C’} \over {BC}}\)
b) Áp dụng: Cho biết \(AH’ = {1 \over 3}AH\) và diện tích tam giác ABC là 67,5 cm2. Tính diện tích tam giác AB’C’.
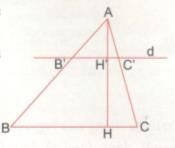

a) ∆ABC có \(H’C’//HC\) \((d//BC,H’,C’ \in d,H \in BC)\)
\( \Rightarrow {{AH’} \over {AH}} = {{AC’} \over {AC}}\) (định lý Thales) (1)
∆ABC có \(B’C’//BC(d//BC;B’,C’ \in d)\)
\( \Rightarrow {{AC’} \over {AC}} = {{B’C’} \over {BC}}\) (hệ quả của định lý Thales) (2)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra \({{AH’} \over {AH}} = {{B’C’} \over {BC}}\)
b) Ta có
\(\left\{ \matrix{ AH \bot BC(AH\,là\,đường\,cao) \hfill \cr B’C’//BC \hfill \cr} \right.\)\(\, \Rightarrow AH \bot B’C’ \)
\(\Rightarrow AH’ \bot B’C'(H’ \in AH)\)
Vì \(AH’ = {1 \over 3}AH \Rightarrow {{AH’} \over {AH}} = {1 \over 3} \)
\(\Rightarrow {{B’C’} \over {BC}} = {{AH’} \over {AH}} = {1 \over 3}\)
Ta có: \({{{S_{AB’C’}}} \over {{S_{ABC}}}} = {{{1 \over 2}AH’.B’C’} \over {{1 \over 2}AH.BC}} = {{AH’} \over {AH}}.{{B’C’} \over {BC}} \)\(\,= {1 \over 3}.{1 \over 3} = {1 \over 9}\)
\(\Rightarrow {{{S_{AB’C’}}} \over {67,5}} = {1 \over 9}\)
Do đó \({S_{AB’C’}} = {{67,5} \over 9} = 7,5(c{m^2})\)
