
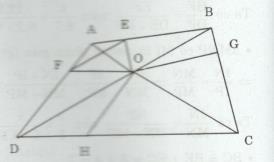
Cho tứ giác ABCD, AC và BD cắt nhau tại O. Đường thẳng qua O và song song với BC cắt AB ở E; đường thẳng song song với CD qua O cắt AD ở F.
a) Chứng minh FE // BD.
b) Từ O kẻ các đường thẳng song song với Ab, AD cắt BD, CD lần lượt tại G và H.
Chứng minh: CG.DH = BG.CH

a) ∆ABC có OE // BC (gt)
\( \Rightarrow {{AE} \over {AB}} = {{AO} \over {AC}}\) (định lý Thales) (1)
Advertisements (Quảng cáo)
∆ADC có OF // CD (gt)
\( \Rightarrow {{AO} \over {AC}} = {{AF} \over {AD}}\) (định lý Thales) (2)
Từ (1) và (2) suy ra \({{AE} \over {AB}} = {{AF} \over {AD}}\)
∆ADB có \({{AE} \over {AB}} = {{AF} \over {FD}} \Rightarrow EF//BD\) (định lý Thales đảo)
b) ∆ABC có OG // AB (gt) \( \Rightarrow {{CG} \over {BG}} = {{CO} \over {AO}}\) (định lý Thales) (3)
∆ACD có OH // AD (gt) \( \Rightarrow {{CO} \over {AO}} = {{CH} \over {DH}}\) (định lý Thales) (4)
Từ (3) và (4) suy ra \({{CG} \over {BG}} = {{CH} \over {DH}} \Rightarrow CG.DH = BG.CH\)
