
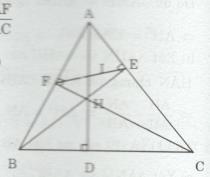
Cho tam giác ABC có ba góc nhọn, các đường cao AD, BE, CF cắt nhai tại H.
a) Chứng minh rằng tam giác AEF đồng dạng với tam giác ABC.
b) Chứng minh rằng AD.HD = DB.DC.
c) Gọi I là giao điểm của AH với EF. Chứng minh rằng tam giác IAF đồng dạng với tam giác IEH.

a) Xét ∆AEB và ∆AFC có: \(\widehat {EAF}\) (chung) và \(\widehat {AEB} = \widehat {AFC}( = 90^\circ )\)
Do đó \(\Delta AEB \sim \Delta AFC(g.g) \)
\(\Rightarrow {{AE} \over {AF}} = {{AB} \over {AC}}\)
\(\Rightarrow {{AE} \over {AB}} = {{AF} \over {AC}}\)
Xét ∆AEF và ∆ABC có: \({{AE} \over {AB}} = {{AF} \over {AC}}\) và góc EAF (chung)
Advertisements (Quảng cáo)
Do đó \(\Delta AEF \sim \Delta ABC(c.g.c)\)
b) Xét ∆ACD và ∆BHD có: \(\widehat {ADC} = \widehat {HDB}( = 90^\circ )\)
Và \(\widehat {CAD} = \widehat {HBD}\) (cùng phụ với góc ACB)
Do đó \(\Delta ACD \sim \Delta BHD(g.g) \)
\(\Rightarrow {{AD} \over {DB}} = {{DC} \over {HD}}\)
\(\Rightarrow AD.HD = DB.DC\)
c) Ta có \(\widehat {AFI} = \widehat {ACB}(\Delta AEF \sim \Delta ABC)\)
Mà \(\widehat {IHE} = \widehat {ACB}\) (cùng phụ với góc HAE) nên \(\widehat {AFI} = \widehat {IHE}\)
Xét ∆IAF và ∆IEH có: \(\widehat {AFI} = \widehat {IHE}\) và \(\widehat {AIF} = \widehat {HIE}\) (đối đỉnh)
Do đó \(\Delta IAF \sim \Delta IEH(g.g)\)
