
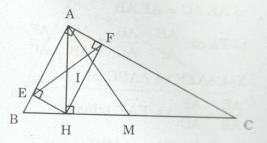
Cho tam giác ABC vuông tại A có đường cao AH. Vẽ HE vuông góc với AB tại E, vẽ HF vuông góc với AC tại F.
a) Chứng minh rằng tam giác AEH và tam giác AHB đồng dạng. Suy ra AH2 = AE.AB.
b) Chứng minh rằng AE.AB = AF.AC.
c) Chứng minh rằng tam giác AFE đồng dạng với tam giác ABC.
d) Gọi AM là trung tuyến của tam giác ABC. Chứng minh \(AM \bot EF\)

a) Xét ∆AEH và ∆AHB có: \(\widehat {EAH}\) (chung) và \(\widehat {AEH} = \widehat {AHB}( = 90^\circ )\)
Do đó \(\Delta AEH \sim \Delta AHB(g.g)\)
\(\Rightarrow {{AH} \over {AB}} = {{AE} \over {AH}} \Rightarrow A{H^2} = AE.AB\)
b) Xét ∆AHF và ∆AHC có:
\(\widehat {HAF}\) (chung) và \(\widehat {AFH} = \widehat {AHC}( = 90^\circ )\)
Do đó \(\Delta AHF \sim \Delta ACH(g.g)\)
Advertisements (Quảng cáo)
\( \Rightarrow {{AH} \over {AC}} = {{AF} \over {AH}} \Rightarrow A{H^2} = AF.AC\)
Mà \(A{H^2} = AE.AB\) nên \(AF.AC = AE.AB\)
c) Xét ∆AFE và ∆ABC có: \({{AE} \over {AC}} = {{AF} \over {AB}}\) (vì AF.AC = AE.AB) và góc A chung
Do đó \(\Delta AFE \sim \Delta ABC(c.g.c)\)
d) Gọi I là giao điểm của EF và AM
∆ABC vuông tại Acos AM là đường trung tuyến (gt)
\( \Rightarrow AM = MC = {{BC} \over 2} \Rightarrow \Delta AMC\) cân tại M \( \Rightarrow \widehat {IAF} = \widehat {ACM}\)
Mà \(\widehat {ACM} = \widehat {AEF}(\Delta ABC \sim \Delta AFE)\) nên \(\widehat {IAF} = \widehat {AEF}\)
Ta có: \(\widehat {AEF} + \widehat {AFI} = 90^\circ (\Delta AEF\) vuông tại A) và \(\widehat {AEF} = \widehat {IAF} \Rightarrow \widehat {IAF} + \widehat {AFI} = 90^\circ \)
Mặt khác \(\widehat {AIF} + \widehat {IAF} + \widehat {AFI} = 180^\circ \) (tổng ba góc trong tam giác IAF)
Nên \(\widehat {AIF} + 90^\circ = 180^\circ \)
\(\Rightarrow \widehat {AIF} = 180^\circ - 90^\circ = 90^\circ\)
\( \Rightarrow AM \bot EF\)
