
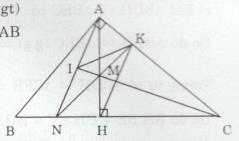
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M và N là trung điểm của AH và BH.
a) Chứng minh rằng tam giác HMN và tam giác HAB đồng dạng
b) Chứng minh rằng HM.HA = HN.HC.
c) Chứng minh rằng tam giác AHN đồng dạng với tam giác AHM.
d) Gọi K là giao điểm của MN với AC, I là giao điểm CN với AN. Chứng minh KM là tia phân giác của góc IKH.

a) M, N lần lượt là trung điểm của AH và BH (gt)
=> MN là đường trung bình của ∆ABH => MN // AB
Xét ∆HMN và ∆HAB có: \(\widehat {MHN}\) (chung)
Và \(\widehat {NMH} = \widehat {BAH}\) (hai góc đồng vị và MN // AB)
Do đó \(\Delta HMN \sim \Delta HAB(g.g)\)
b) Ta có: \(\widehat {ABC} = \widehat {HAC}\) (cùng phụ với góc C)
Và \(\widehat {ABC} = \widehat {MNH}\) (hai góc đồng vị và MN // AB) \( \Rightarrow \widehat {HAC} = \widehat {MNH}\)
Xét ∆HAC và ∆HNM có: \(\widehat {HAC} = \widehat {MNH}\) và \(\widehat {AHC} = \widehat {MHN}( = 90^\circ )\)
Do đó \(\Delta HAC \sim \Delta HNM(g.g) \)
\(\Rightarrow {{HA} \over {HN}} = {{HC} \over {HM}}\)
\(\Rightarrow HM.HA = HN.HC\)
Advertisements (Quảng cáo)
c) Xét ∆ANH và ∆MHC có: \({{AH} \over {CH}} = {{HN} \over {HM}}\) (vì HM.HA=HN.HC)
Và \(\widehat {AHN} = \widehat {MHC}( = 90^\circ )\)
\(\Rightarrow \Delta ANH \sim \Delta CMH(c.g.c)\)
d) Ta có MN // AB, \(AB \bot AC \Rightarrow MN \bot AC\)
∆ANC có AH, NK là hai đường cao cắt nhau tại M
=> M là trực tâm của tam giác ANC
=> CM là đường cao của tam giác ANC \( \Rightarrow CM \bot AN\)
Xét ∆AKN và ∆AIC có: \(\widehat {KAN}\) (chung) và \(\widehat {AKN} = \widehat {AIC}( = 90^\circ )\)
Do đó \(\Delta AKN \sim \Delta AIC(g.g) \)
\(\Rightarrow {{AK} \over {AI}} = {{AN} \over {AC}}\)
\(\Rightarrow {{AK} \over {AN}} = {{AI} \over {AC}}\)
Xét ∆AKI và ∆ABC có: \({{AK} \over {AN}} = {{AI} \over {AC}},\widehat {KAI}(chung)\)
Do đó \(\Delta AKI \sim \Delta ANC(c.g.c) \)
\(\Rightarrow \widehat {AKI} = \widehat {ANC}\)
Tương tự \(\Delta CKH \sim \Delta CNA \Rightarrow \widehat {CKH} = \widehat {ANC}\)
Ta có \(\widehat {AKI} = \widehat {CKH}( = \widehat {ANC})\) mà \(\widehat {AKI} + \widehat {MKI} = \widehat {CKM} + \widehat {MKH}( = 90^\circ )\)
Do đó \(\widehat {MKI} = \widehat {MKH} \Rightarrow KM\) là tia phân giác của góc IKH
