
Cho hình thang cân ABCD có diện tích 50 cm2 và M, N, P, Q lần lượt là trung điểm của các cạnh.
a) Tứ giác MNPQ là hình gì ?
b) Tính diện tích tứ giác MNPQ.

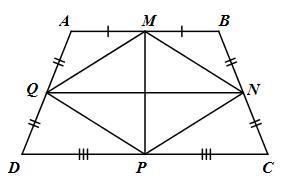
a) M, N lần lượt là trung điểm của AB và BC (gt)
\( \Rightarrow MN\) là đường trung bình của tam giác ABC \( \Rightarrow MN//AC\) và \(MN = {{AC} \over 2}\,\,\left( 1 \right)\)
Q, P lần lượt là trung điểm của AD và CD (gt)
\( \Rightarrow QP\) là đường trung bình của tam giac ADC \( \Rightarrow QP//AC\) và \(QP = {{AC} \over 2}\,\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow MN = QP\) và \(MN//QP\)
Advertisements (Quảng cáo)
Suy ra tứ giác MNPQ là hình bình hành.
Q, M lần lượt là trung điểm của AD và AB (gt)
\( \Rightarrow QM\) là đường trung bình của tam giác ABD \( \Rightarrow QM = {{BD} \over 2}\)
Mà \(MN = {{AC} \over 2}\) và \(BD = AC\) (ABCD là hình thang cân) nên \(QM = MN\)
Hình bình hành MNPQ có \(QM = MN\) nên là hình thoi.
b) Hình thang ABCD (AB // CD) có Q, N lần lượt là trung điểm của AD và BC (gt)
\( \Rightarrow QN\) là đường trung bình của hình thang ABCD \( \Rightarrow QN = {{AB + CD} \over 2}\) và \(QN // DC\)
Ta có \(QN \bot MP\) (MNPQ là hình thoi) và QN // DC \( \Rightarrow MP \bot DC \Rightarrow MP\) là đường cao của hình thang ABCD.
\({S_{MNPQ}} = MP.QN = MP.{{AB + CD} \over 2} = {{MP\left( {AB + CD} \right)} \over 2} = {S_{ABCD}} = 50\,\,\left( {c{m^2}} \right)\)
