
Cho hình bình hành ABCD với AD = 2AB. Từ C vẽ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE, MF cắt BC tại N.
a) Tứ giác MNCD là hình gì ?
b) Tam giác EMC là tam giác gì ?
c) Chứng minh : \(\widehat {BAD} = 2\widehat {AEM}\) .
HD: b) MF // DC suy ra F là trung điểm của EC.
c) \(\widehat {AEM} = \widehat {EMN} = \widehat {NMC} = \widehat {MCD} = {1 \over 2}\widehat {NCD}\) .

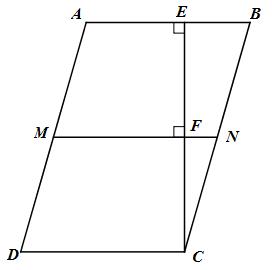
a) Ta có \(MN \bot CE\,\,\left( {gt} \right);\,\,AB \bot CE\,\,\left( {gt} \right) \Rightarrow MN//AB\)
Mà AB // CD (ABCD là hình bình hành) nên MN // CD
Tứ giác MNCD có MN // CD
Và MD // CN (AD // BC, \(M \in AD,\,\,N \in BC\))
Do đó tứ giác MNCD là hình bình hành.
b) Gọi F là giao điểm của MN và EC
Hình thang AECD (EC // CD) có \(MF // AE // CD\)
Advertisements (Quảng cáo)
Và M là trung điểm của AD (gt)
\( \Rightarrow F\) là trung điểm của EC.
\(\Delta MEC\) có MF là đường trung tuyến (F là trung điểm của EC)
Và MF là đường cao \(\left( {MF \bot EC} \right) \Rightarrow \Delta MEC\) cân tại M.
c) Ta có \(AD = 2AB\,\,\left( {gt} \right)\)
\(AD = 2MD\) (M là trung điểm của AD)
Và \(AB = CD\) (ABCD là hình bình hành) \( \Rightarrow MD = CD\).
Hình bình hành MNCD có \(MD = CD\) nên là hình thoi.
\( \Rightarrow CM\) là đường phân giác \( \Rightarrow \widehat {EMF} = \widehat {CMF}\)
Mà \(\widehat {EMF} = \widehat {AEM}\) (hai góc so le trong và AE // MF)
Và \(\widehat {CMF} = \widehat {MCD}\) (hai góc so le trong và MF // CD)
Nên \(\widehat {AEM} = \widehat {MCD}\)
Ta có \(\widehat {AEM} = \widehat {MCD};\,\,2\widehat {MCD} = \widehat {NCD}\) (CM là tia phân giác của \(\widehat {NCD}\))
Và \(\widehat {NCD} = \widehat {BAD}\) (ABCD là hình bình hành) \( \Rightarrow 2\widehat {AEM} = \widehat {BAD}\).
