
Cho hình bình hành ABCD. Lấy E, F trên AC sao cho AE = EF = FC.
a) Chứng minh rằng tứ giác BEDF là hình bình hành.
b) Gọi M là giao điểm của BC avf DF. Chứng minh rằng \(FM = {1 \over 2}FD\) .
c) Gọi I là giao điểm của CD và BF, J là giao điểm của AB và DE. Chứng minh rằng ba điểm I, O, J thẳng hàng.

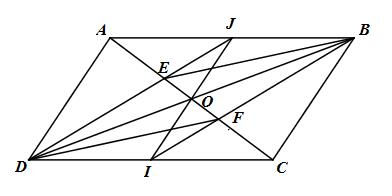
a) O là giao điểm của AC và BD.
Tứ giác ABCD là hình bình hành (gt)
\( \Rightarrow O\) là trung điểm của AC và BD \( \Rightarrow OA = OC\).
\( \Rightarrow OA - AE = OC - FC\) (vì \(AE = FC\))
\( \Rightarrow EO = FO \Rightarrow O\) là trung điểm của EF.
Tứ giác DEBF có DB cắt EF tại O.
O là trung điểm của DB và O là trung điểm của EF.
Do đó tứ giác DEBF là hình bình hành.
Advertisements (Quảng cáo)
b) \(\Delta EBC\) có EB // FM (EB // DF, \(M \in DF\)) và F là trung điểm của EC \(\left( {EF = FC} \right)\)
\( \Rightarrow M\) là trung điểm của BC.
\(\Delta DBC\) có DM cắt AC tại F (gt),
DM là đường trung tuyến (M là trung điểm của BC)
Và CO là đường trung tuyến (O là trung điểm của DB)
\( \Rightarrow F\) là trọng tâm của tam giác DBC.
\( \Rightarrow MF = {1 \over 3}DM\) và \(FD = {2 \over 3}DM \Rightarrow {{MF} \over {FD}} = {{{1 \over 3}DM} \over {{2 \over 3}DM}} = {1 \over 2} \Rightarrow MF = {1 \over 2}FD\).
c) Tứ giác JBID có DJ // BI (DE // BF, \(J \in DE,I \in BF\))
và \(JB//DI\,\,\left( {AB//CD,\,\,J \in AB,\,\,I \in CD} \right)\)
Do đó tứ giác JBID là hình bình hành
\( \Rightarrow JI\) cắt DB tại trung điểm của mỗi đường.
Mà O là trung điểm của DB (câu a) nên O là trung điểm của JI.
Vậy I, O, J thẳng hàng.
