Cho khối lăng trụ tứ giác đều ABCD.A1B1C1D1 có khoảng cách giữa hai đường thẳng AB và A1D bằng 2 và độ dài đường chéo của mặt bên bằng 5.
a)Hạ \(AK \bot {A_1}D\left( {K \in {A_1}D} \right)\). Chứng minh rằng AK=2.
b)Tính thể tích khối lăng trụ ABCD.A1B1C1D1.

(H.6)
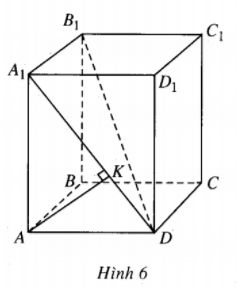
a)
\(\eqalign{ & AB//{A_1}{B_1} \Rightarrow AB// \left( {{A_1}{B_1}D} \right) \cr & \Rightarrow {d_{\left( {A,\left( {{A_1}{B_1}D} \right)} \right)}} = {d_{\left( {AB,{A_1}D} \right)}}. \cr & \cr} \)
Ta có :
\(\eqalign{ & {A_1}{B_1} \bot \left( {A{A_1}{D_1}D} \right) \cr & \Rightarrow {A_1}{B_1} \bot AK. \cr} \)
Advertisements (Quảng cáo)
Mặt khác \({A_1}D \bot AK,\) suy ra \(AK \bot \left( {{A_1}{B_1}D} \right)\)
Vậy \(AK = d\left( {A,\left( {{A_1}{B_1}D} \right)} \right) = d\left( {AB,{A_1}D} \right) = 2\)
b) Xét tam giác vuông \({A_1}AD\), ta có :
\(A{K^2} = {A_1}K.KD.\)
Đặt A1K = x \(4 = x\left( {5 - x} \right) \Rightarrow {x^2} - 5x + 4 = 0 \Rightarrow \left[ \matrix{ x = 1 \hfill \cr x = 4 \hfill \cr} \right.\)
Với x=1, \(AD = \sqrt {A{K^2} + K{D^2}} = 2\sqrt 5 \)
\({\rm{A}}{{\rm{A}}_1} = \sqrt {{A_1}{D^2} - A{D^2}} = \sqrt 5 \)
Khi đó \({V_{ABCD.{A_1}{B_1}{C_1}{D_1}}} = 20\sqrt 5 \)
Với x=4, tương tự ta có :\({V_{ABCD.{A_1}{B_1}{C_1}{D_1}}} = 10\sqrt 5 \).
