Cho khối lăng trụ đứng \(ABCD.{A_1}{B_1}{C_1}{D_1}\) có đáy hình bình hành và góc \(BAD = {45^0}\). Các đường chéo AC1 và DB1 lần lượt tạo với đáy những góc 450 và 600. Hãy tính thể tích của khối lăng trụ nếu biết chiều cao của nó bằng 2.

(h.8)
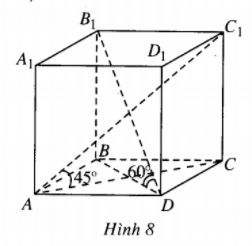
Hình lăng trụ đã cho là hình lăng trụ đứng nên các cạnh bên vuông góc với đáy và độ dài cạnh bên bằng chiều cao của hình lăng trụ. Từ giả thiết ta suy ra :
Góc \({C_1}AC = {45^0}\),góc \({B_1}DB = {60^0}\).
Advertisements (Quảng cáo)
Từ đó suy ra
\(AC = C{C_1} = 2,BD = 2\cot {60^0} = {2 \over {\sqrt 3 }}.\)
Áp dụng định lý hàm số côsin ta có :
\(\eqalign{ & B{D^2} = A{B^2} + A{D^2} - 2AB.AD.\cos {45^0}, \cr & A{C^2} = D{C^2} + A{D^2} - 2DC.AD.\cos {135^0}, \cr} \)
Từ đó ta có:
\(\eqalign{ & B{D^2} - A{C^2} = - AB.AD.\sqrt 2 + DC.AD.\left( { - \sqrt 2 } \right)\cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - 2\sqrt 2 AB.AD \cr & \Rightarrow {4 \over 3} - 4 = - 2\sqrt 2 AB.AD \cr&\Rightarrow AB.AD = {8 \over {3.2\sqrt 2 }} = {4 \over {3\sqrt 2 }}. \cr & {V_{ABCD.{A_1}{B_1}{C_1}{D_1}}} = AB.AD.\sin {45^0}{\rm{.A}}{{\rm{A}}_1} \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;= {4 \over {3\sqrt 2 }}.{{\sqrt 2 } \over 2}.2 = {4 \over 3}. \cr} \)
