Cho hình lập phương ABCD.A’B’C’D’ có cạnh 1. Gọi M, N, P lần lượt là trung điểm của các cạnh B’B, CD và A’D’.
a) Tính khoảng cách giữa cặp đường thẳng A’B, B’D và cặp đường thẳng PI, AC’ (I là tâm của đáy ABCD).
b) Tính góc giữa hai đường thẳng MP và C’N.
Tính góc giữa hai mặt phẳng (PAI) và (DCC’D’).

a) Ta chọn hệ trục Oxyz sao cho gốc toa độ là A, Tia Ox chứa AB, tia Oy chứa AD và tia Oz chứa AA’(h.103).
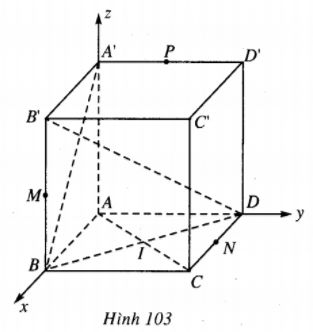
Khi đó
\(\eqalign{ & A = \left( {0;0;0} \right),B = \left( {1;0;0} \right) \cr & D = \left( {0;1;0} \right),A’ = \left( {0;0;1} \right) \cr & C = \left( {1;1;0} \right),B’ = \left( {1;0;1} \right) \cr & C’ = \left( {1;1;1} \right),D’ = \left( {0;1;1} \right). \cr} \)
Suy ra \(\overrightarrow {A’B} = \left( {1;0; - 1} \right)\)
\(\overrightarrow {B’D} = \left( { - 1; 1; - 1} \right)\)
\( \Rightarrow \left[ {\overrightarrow {A’B} ,\overrightarrow {B’D} } \right] = \left( {1;2;1} \right).\)
Advertisements (Quảng cáo)
\(\overrightarrow {A’B’} = \left( {1;0;0} \right)\)
\(d\left( {A’B,B’D} \right) = {{\left| {\left[ {\overrightarrow {A’B} ,\overrightarrow {B’D} } \right].\overrightarrow {A’B’} } \right|} \over {\left| {\left[ {\overrightarrow {A’B} ,\overrightarrow {B’D} } \right]} \right|}} = {1 \over {\sqrt 6 }}.\)
Ta lại có :
\(\eqalign{ & \cr & P = \left( {0;{1 \over 2};1} \right),I = \left( {{1 \over 2};{1 \over 2};0} \right),\cr&\overrightarrow {IP} = \left( { - {1 \over 2};0;1} \right). \cr & \overrightarrow {AC’} = \left( {1;1;1} \right),\overrightarrow {AP} = \left( {0;{1 \over 2};1} \right) \cr} \)
Suy ra \(d\left( {PI,AC’} \right) = {{\left| {\left[ {\overrightarrow {IP} ,\overrightarrow {AC’} } \right].\overrightarrow {AP} } \right|} \over {\left| {\left[ {\overrightarrow {IP} ,\overrightarrow {AC’} } \right]} \right|}} = {{\sqrt {14} } \over {28}}.\)
b) Ta có \(M = \left( {1;0;{1 \over 2}} \right),N = \left( {{1 \over 2};1;0} \right)\)
\(\eqalign{ & \Rightarrow \overrightarrow {MP} = \left( { - 1;{1 \over 2};{1 \over 2}} \right),\overrightarrow {NC’} = \left( {{1 \over 2};0;1} \right) \cr & \Rightarrow \overrightarrow {MP} .\overrightarrow {NC’} = 0 \Rightarrow MP \bot NC’. \cr} \)
Mặt phẳng (PIA) có vectơ pháp tuyến: \(\overrightarrow n = \left[ {\overrightarrow {AP} ,\overrightarrow {AI} } \right] = \left( { - {1 \over 2};{1 \over 2}; - {1 \over 4}} \right).\)
Mặt phẳng (DCC’D’) có vectơ pháp tuyến là \(\overrightarrow {AD} = \left( {0;1;0} \right).\)
Gọi \(\varphi \) là góc giữa hai mặt phẳng trên thì
\(\cos \varphi = {{\left| {\overrightarrow n .\overrightarrow {AD} } \right|} \over {\left| {\overrightarrow n } \right|.\left| {\overrightarrow {AD} } \right|}} = {2 \over 3}.\)
